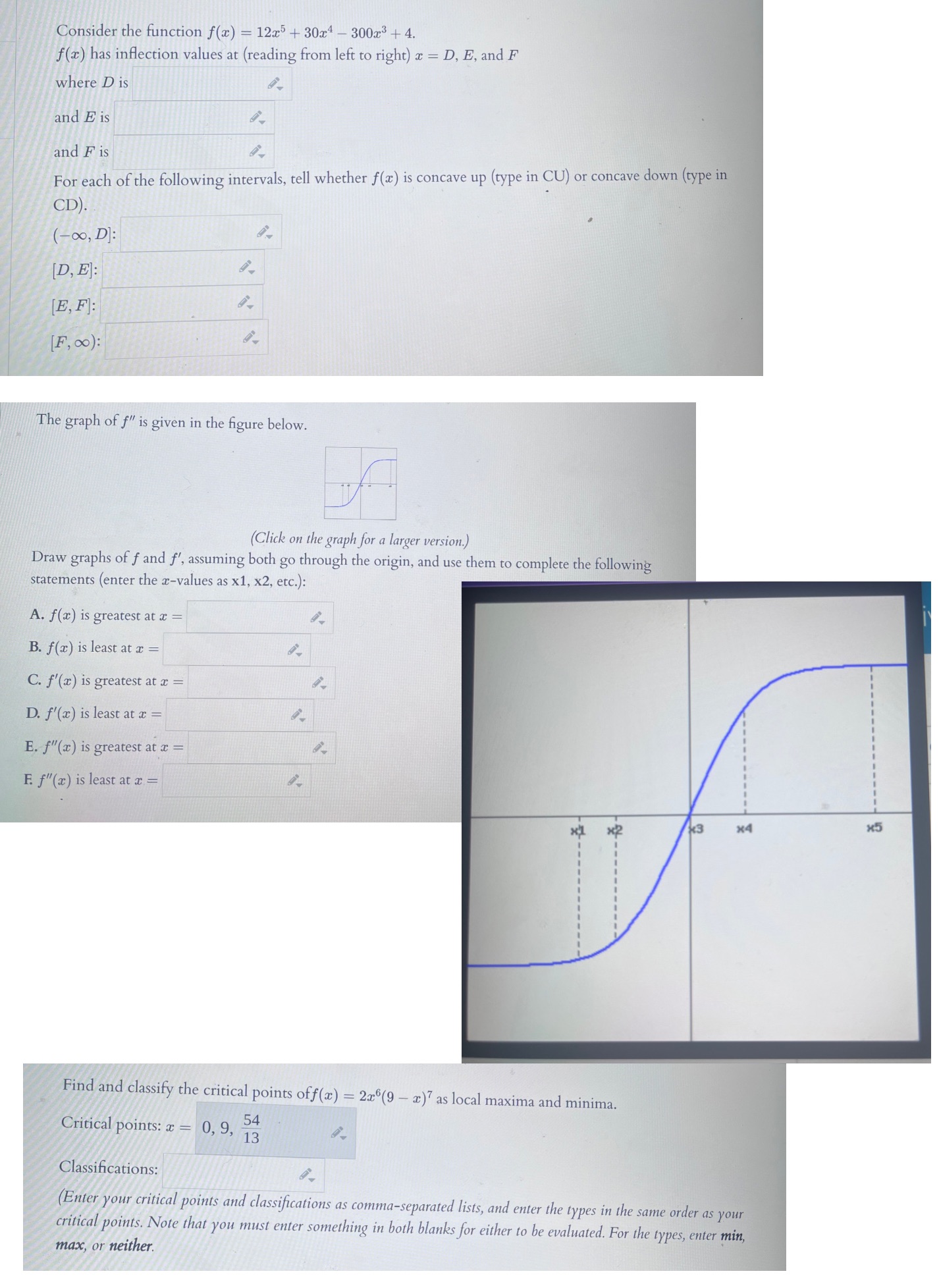
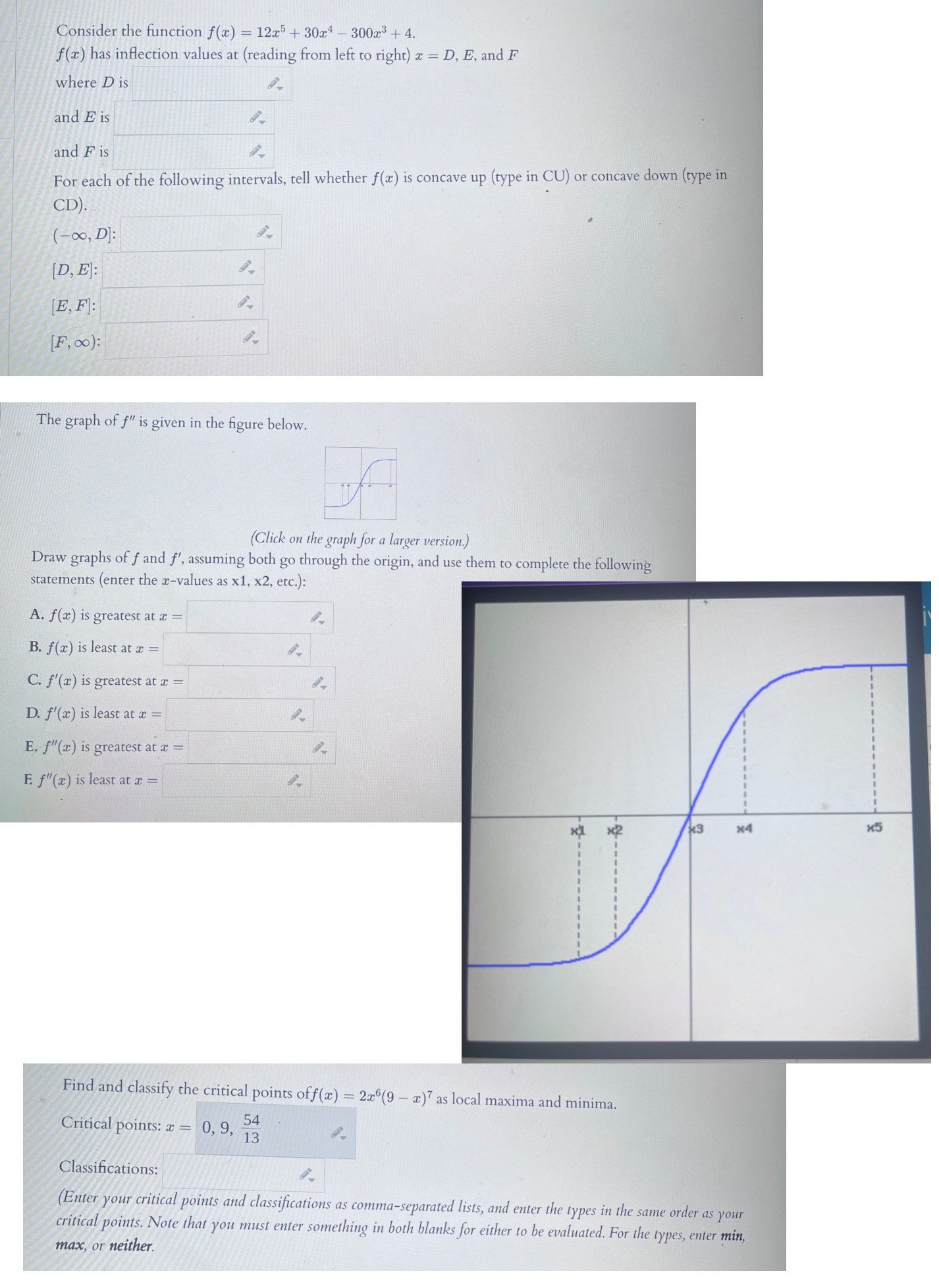
Consider the function f(x) = 12x5 + 30x4 - 30023 + 4. f(a) has inflection values at (reading from left to right) x = D, E, and F where D is and E is and F is For each of the following intervals, tell whether f(x) is concave up (type in CU) or concave down (type in CD). (- 0o, D]: [D, E]: [E, F]: [F, 00): The graph of f" is given in the figure below. (Click on the graph for a larger version.) Draw graphs of f and f', assuming both go through the origin, and use them to complete the following statements (enter the x-values as x1, x2, etc.): A. f(x) is greatest at x = B. f(x) is least at x = C. f'(x) is greatest at x = D. f'(x) is least at a = E. f"(x) is greatest at x = F. f"(x) is least at x = *2 x4 x5 Find and classify the critical points off(x) = 2x6(9 - x) as local maxima and minima. Critical points: x = 0, 9, 54 13 Classifications: Enter your critical points and classifications as comma-separated lists, and enter the types in the same order as your critical points. Note that you must enter something in both blanks for either to be evaluated. For the types, enter min, max, or neither