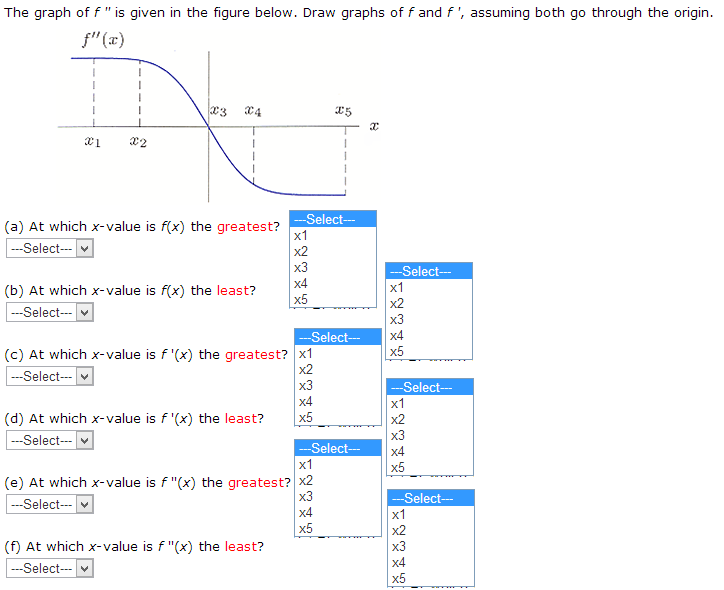
Consider the function f(x) = 2sin(x2) on the interval 0 x 3. (a) Find the exact value in the given interval where an antiderivative, F, reaches its maximum. X = (b) If F(1) = 9, estimate the maximum value attained by F. (Round your answer to three decimal places.) y= The graph of f" is given in the figure below. Draw graphs of f and f', assuming both go through the origin. f"(x) 1 I X1 X2 x3 34 (a) At which x-value is f(x) the greatest? ---Select--- (b) At which x-value is f(x) the least? ---Select--- (d) At which x-value is f'(x) the least? ---Select--- (c) At which x-value is f '(x) the greatest? |x1 ---Select--- x2 x3 x4 x5 (f) At which x-value is f"(x) the least? ---Select--- ---Select--- x1 x2 x3 x4 x5 25 ---Select--- X 1 x1 (e) At which x-value is f"(x) the greatest? x2 ---Select--- x3 x4 x5 -Select--- x ---Select--- x1 x2 x3 x4 x5 ---Select--- x1 x2 x3 x4 x5 ---Select--- x1 x2 x3 x4 x5 Let G be a function whose derivative is shown below. Assume the domains of G and G'are 0 x 12. G(x) 8 4 0 -4 -8 co JAN 10. 12 Answer each of the following questions abo G. Each part is independent of the other parts. (a) Find G(6), if we know that G(0) = 0. G(6) = (b) Find the coordinates of the local minimum of G, if we know that G(0) = 22. )