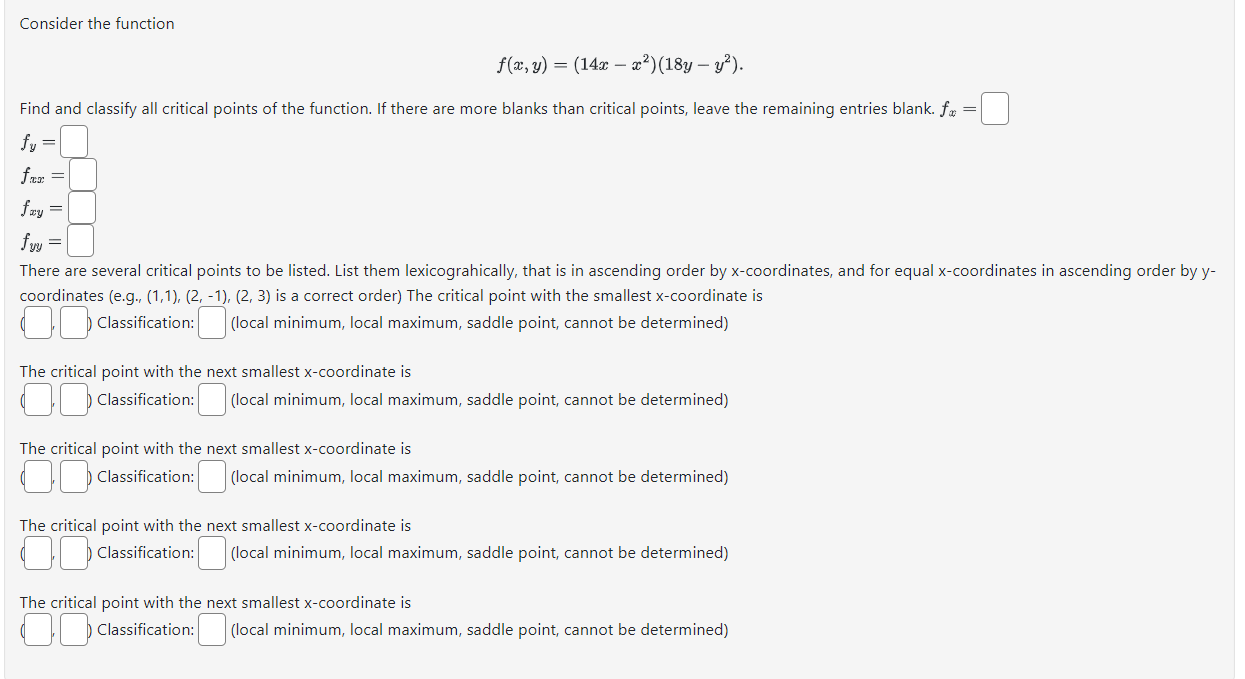
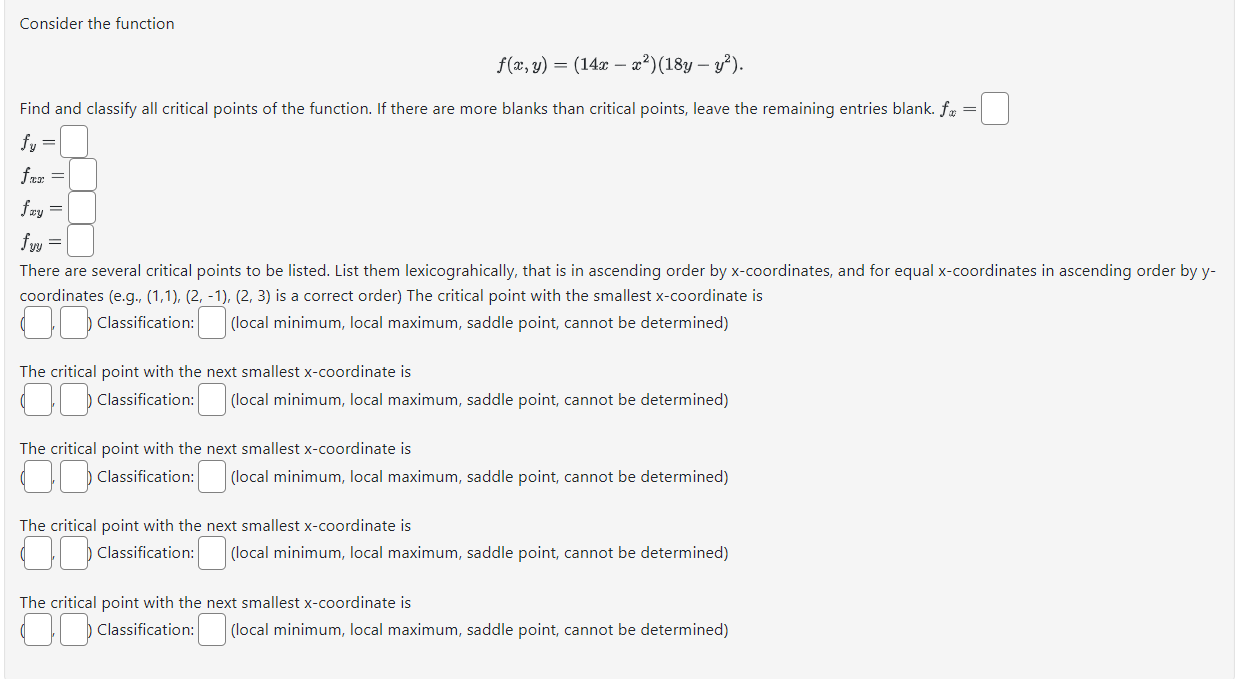
Consider the function f(x, y) = (14x - x2)(18y - y?). Find and classify all critical points of the function. If there are more blanks than critical points, leave the remaining entries blank. fx fy = fax = fzy = fyy = There are several critical points to be listed. List them lexicograhically, that is in ascending order by x-coordinates, and for equal x-coordinates in ascending order by y- coordinates (e.g., (1,1), (2, -1), (2, 3) is a correct order) The critical point with the smallest x-coordinate is Classification: (local minimum, local maximum, saddle point, cannot be determined) The critical point with the next smallest x-coordinate is Classification: (local minimum, local maximum, saddle point, cannot be determined) The critical point with the next smallest x-coordinate is Classification: (local minimum, local maximum, saddle point, cannot be determined) The critical point with the next smallest x-coordinate is Classification: (local minimum, local maximum, saddle point, cannot be determined) The critical point with the next smallest x-coordinate is Classification: (local minimum, local maximum, saddle point, cannot be determined)Compute the starting and ending positions [at timest : 0 and t = 1, respectively} for the path of motion described by the following vectorvalued function. ' Function: t} = (Bit, 39,49 5) Starting point: (D,DD Ending point: (D.D.U Now compute the derivative of that same vectorvalued function. Answer: (D.D,C]) Now compute the starting and ending velocities for that same vectorvalued function. Starting velocity: {ODD} Ending velocity: {Elgal