Consider the function

g

defined by

g(x)=(x^(2)-4)/(|x-2|)

for

x!=2

\ Our goal is to understand the behavior of

g

near

x=2

\ a) As

x

approaches 2 this gives an indeterminate form of the type\

0^(0)

(0)/(0)

0\\\\times \\\\infty

\\\\infty -\\\\infty

(\\\\infty )/(\\\\infty )

1^(\\\\infty )

\ Suppose first that

x>2

\ b) If

x>2

, then

|x-2|=

\

a^(b),(a)/(b),\\\\sqrt(a),|a,\\\\pi ,sin(a)

|

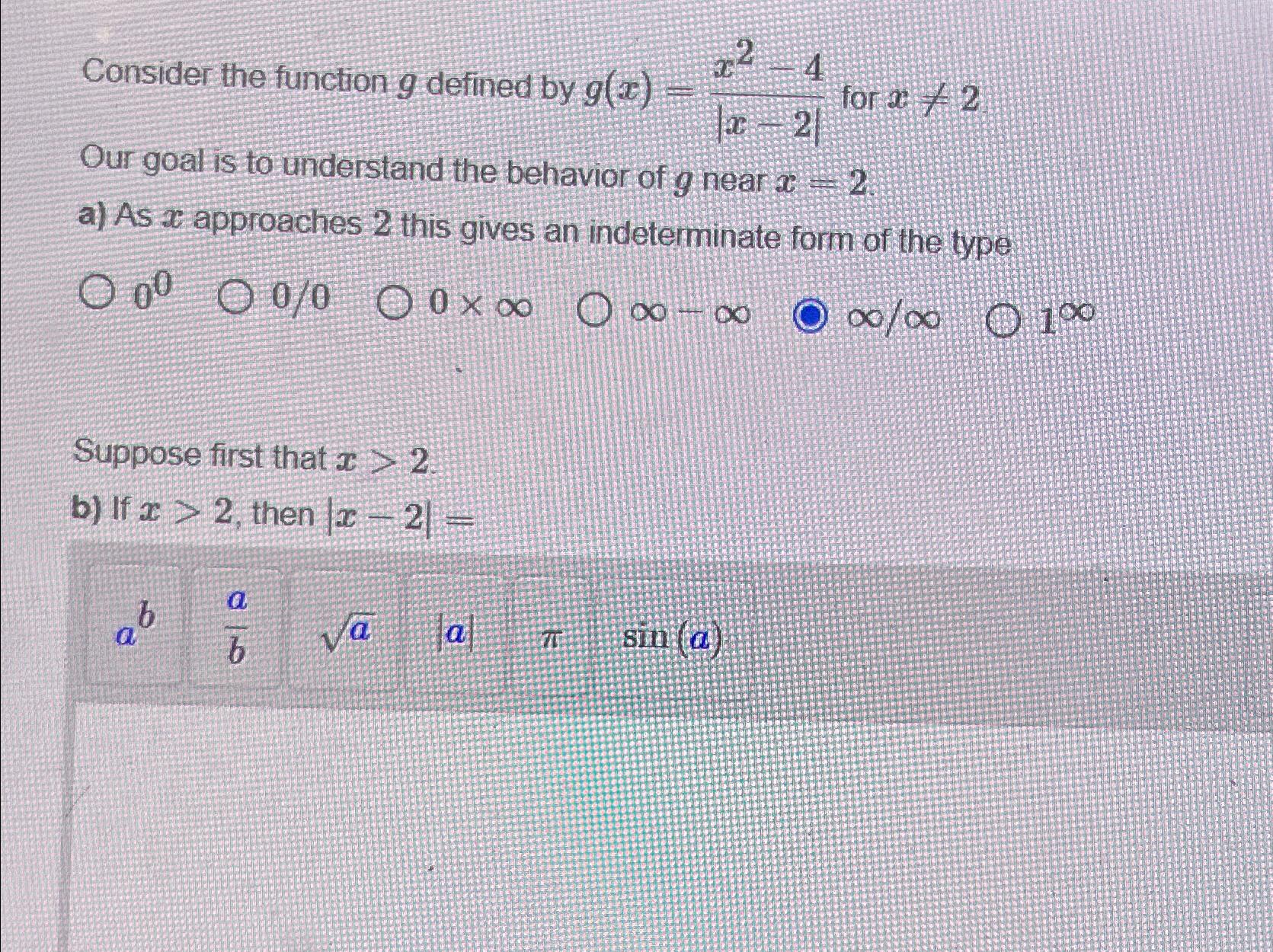
Consider the function g defined by g(x)=x2x24 for x=2 Our goal is to understand the behavior of g near x=2 a) As x approaches 2 this gives an indeterminate form of the type 00 0/0 0 / 1 Suppose first that x>2 b) If x>2, then x2=