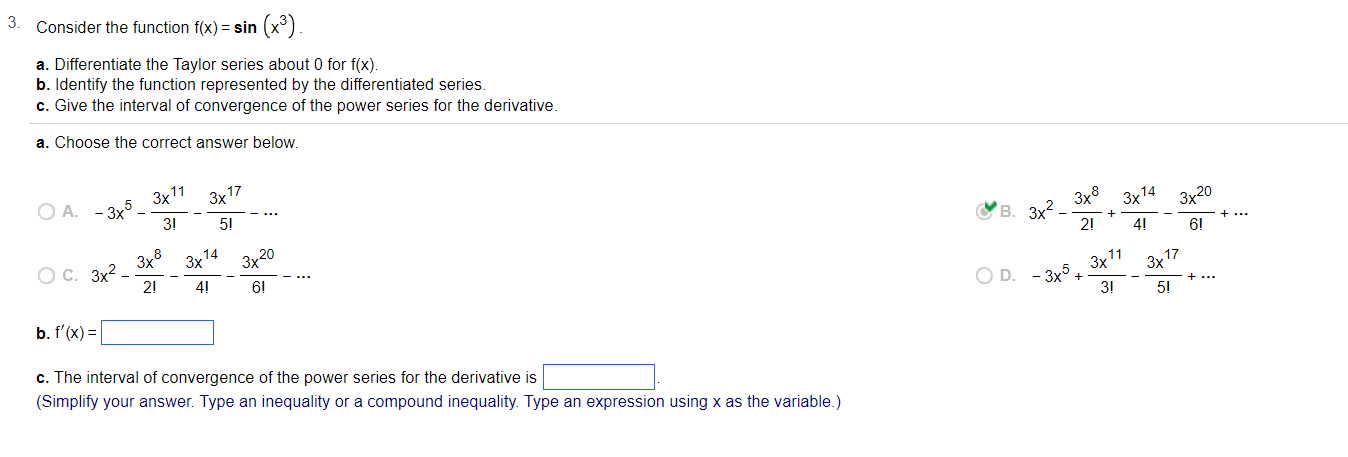
Question: Consider the function l(x} : sin (x3) . a. Differentiate the Taylor series about t] for f(x). b. Identify the function represented by the dllterentiated
![Taylor series about t] for f(x). b. Identify the function represented by](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667d0b95b2820_997667d0b95a1a09.jpg)
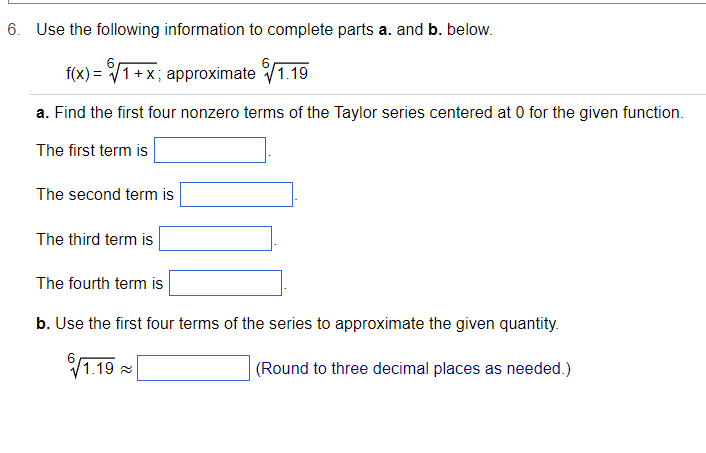
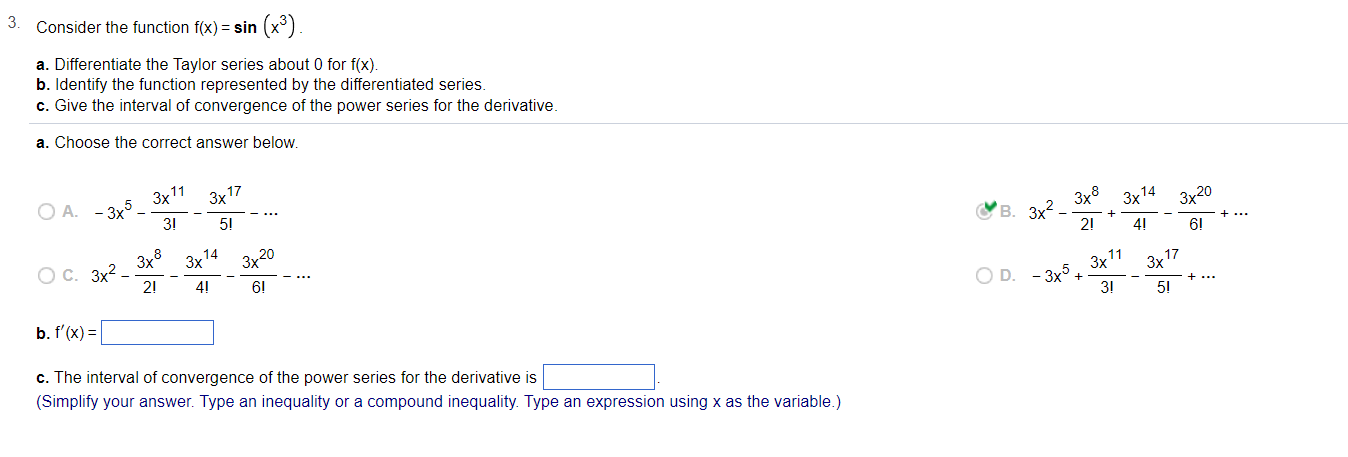

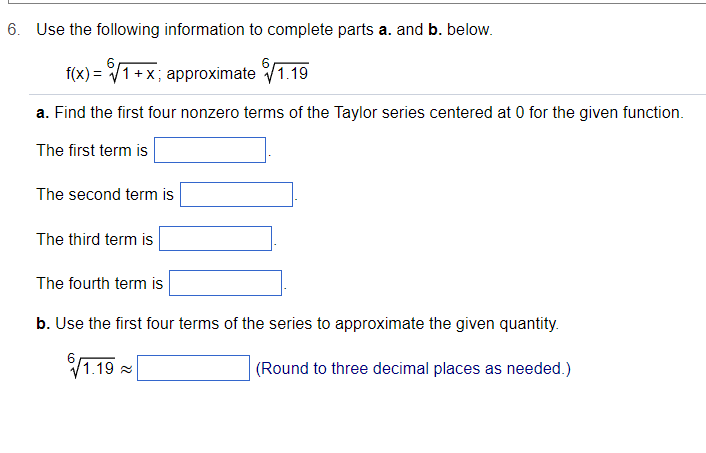
Consider the function l(x} : sin (x3) . a. Differentiate the Taylor series about t] for f(x). b. Identify the function represented by the dllterentiated series, c. Give the interval of convergence of the power series for the derivative, a. Choose the correct answer below. 3x11 3x1? 3x3 _ 5_ _ __., .v 2_7 A 3" 3! 5! B. 3x 2! + _ _ c 2 3x8 3x\" 3x20 _ _ o 5 3x ' . 3X _ 72! _ 74! _ 76! _ .7 . -3)( + 73! b.f'(x)= c. The interval of convergence of the power series for the derivative is (Simplify your answer, Type an Inequality or a compound inequality, Type an expression usmg x as the variable) 4. Consider the function f(x) = 5 tan - 1(x). a. Differentiate the Taylor series about 0 for f(x). b. Identify the function represented by the differentiated series. c. Give the interval of convergence of the power series for the derivative. a. Choose the correct answer below. O A. - 5+5x2 - 5x4 + 5x6 -... 5x3 5x O B. 5x - 5 + X 3 7 5x3 5x/ O C. 5x + 5 + X' + 3 7 O D. 5-5x2 + 5x4 - 5x6 + ... b. f' (x ) = c. The interval of convergence of the power series of f'(x) is (Simplify your answer. Type an inequality or a compound inequality. Type an expression using x as the variable.)6. Use the following information to complete parts a. and b. below. f(x) = V1 + x; approximate #1.19 a. Find the first four nonzero terms of the Taylor series centered at 0 for the given function. The first term is The second term is The third term is The fourth term is b. Use the first four terms of the series to approximate the given quantity. 6 1 1.19 ~ (Round to three decimal places as needed.)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


