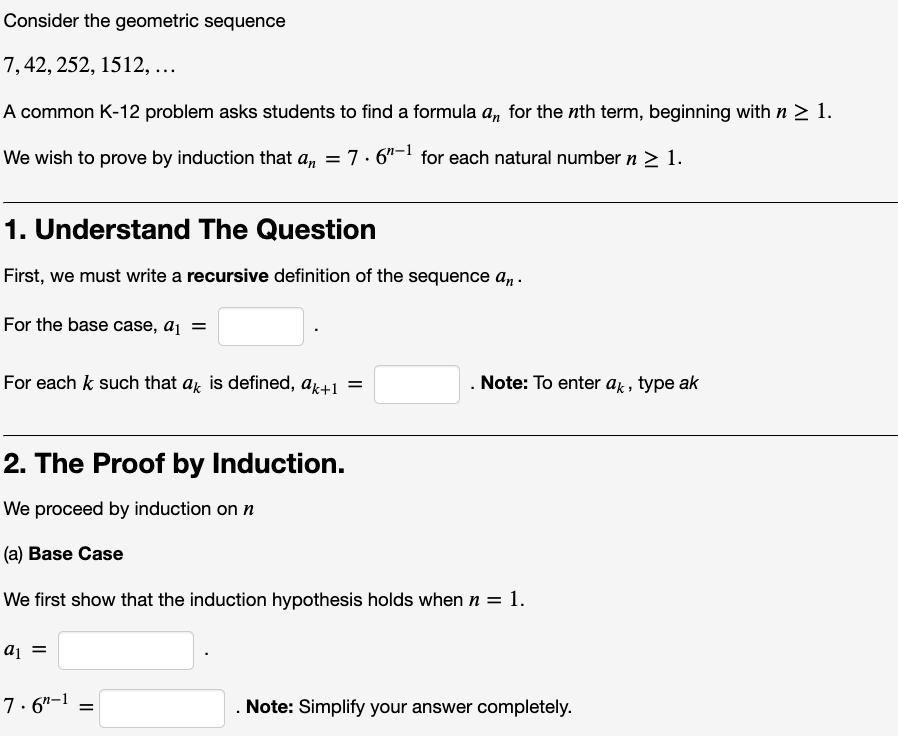
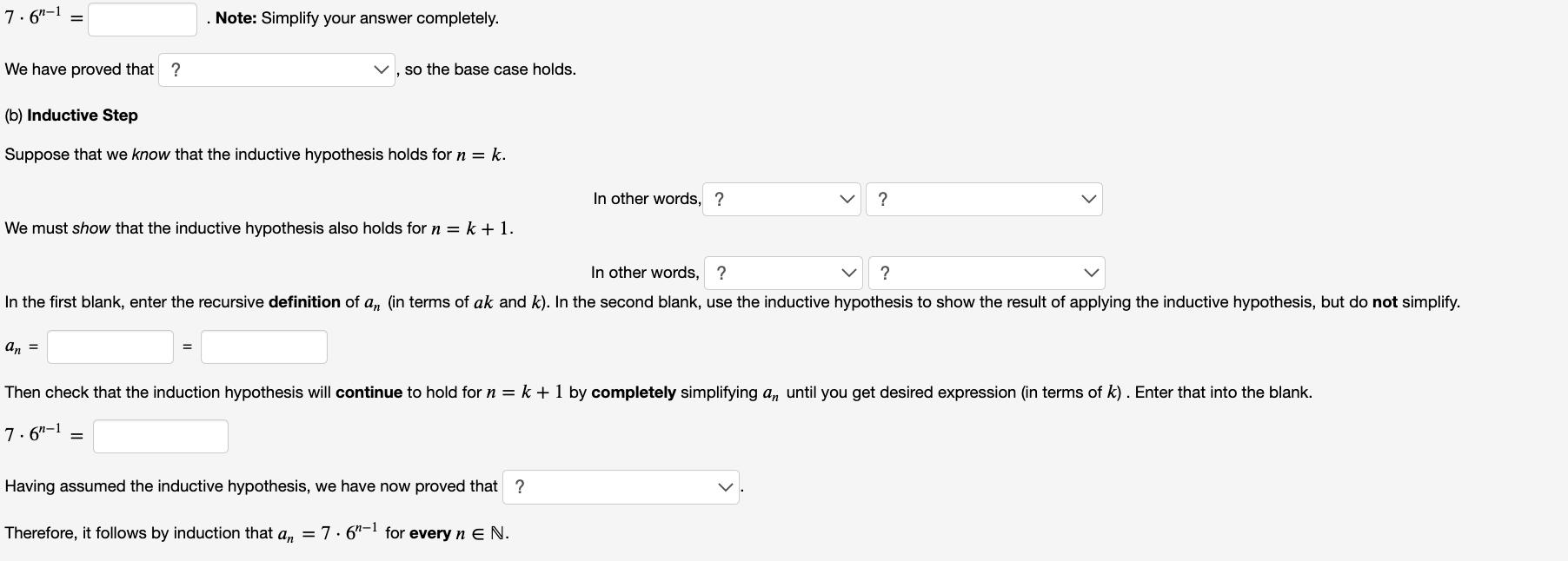
Consider the geometric sequence 7, 42, 252, 1512, ... A common K-12 problem asks students to find a formula an for the nth term, beginning with n 1. 7.6"-1 for each natural number n 1. We wish to prove by induction that an = 1. Understand The Question First, we must write a recursive definition of the sequence an. For the base case, a = For each k such that ak is defined, ak+1 = 2. The Proof by Induction. We proceed by induction on n (a) Base Case We first show that the induction hypothesis holds when n = 1. a = Note: To enter ak, type ak 7.6"-1 = Note: Simplify your answer completely. 7.6"-1 = We have proved that ? Note: Simplify your answer completely. , so the base case holds. (b) Inductive Step Suppose that we know that the inductive hypothesis holds for n = k. an = We must show that the inductive hypothesis also holds for n=k + 1. In other words, ? In other words, ? ? In the first blank, enter the recursive definition of an (in terms of ak and k). In the second blank, use the inductive hypothesis to show the result of applying the inductive hypothesis, but do not simplify. ? Having assumed the inductive hypothesis, we have now proved that ? Therefore, it follows by induction that a, = 7.6"-1 for every n E N. Then check that the induction hypothesis will continue to hold for n = k + 1 by completely simplifying an until you get desired expression (in terms of k). Enter that into the blank. 7.6"-1