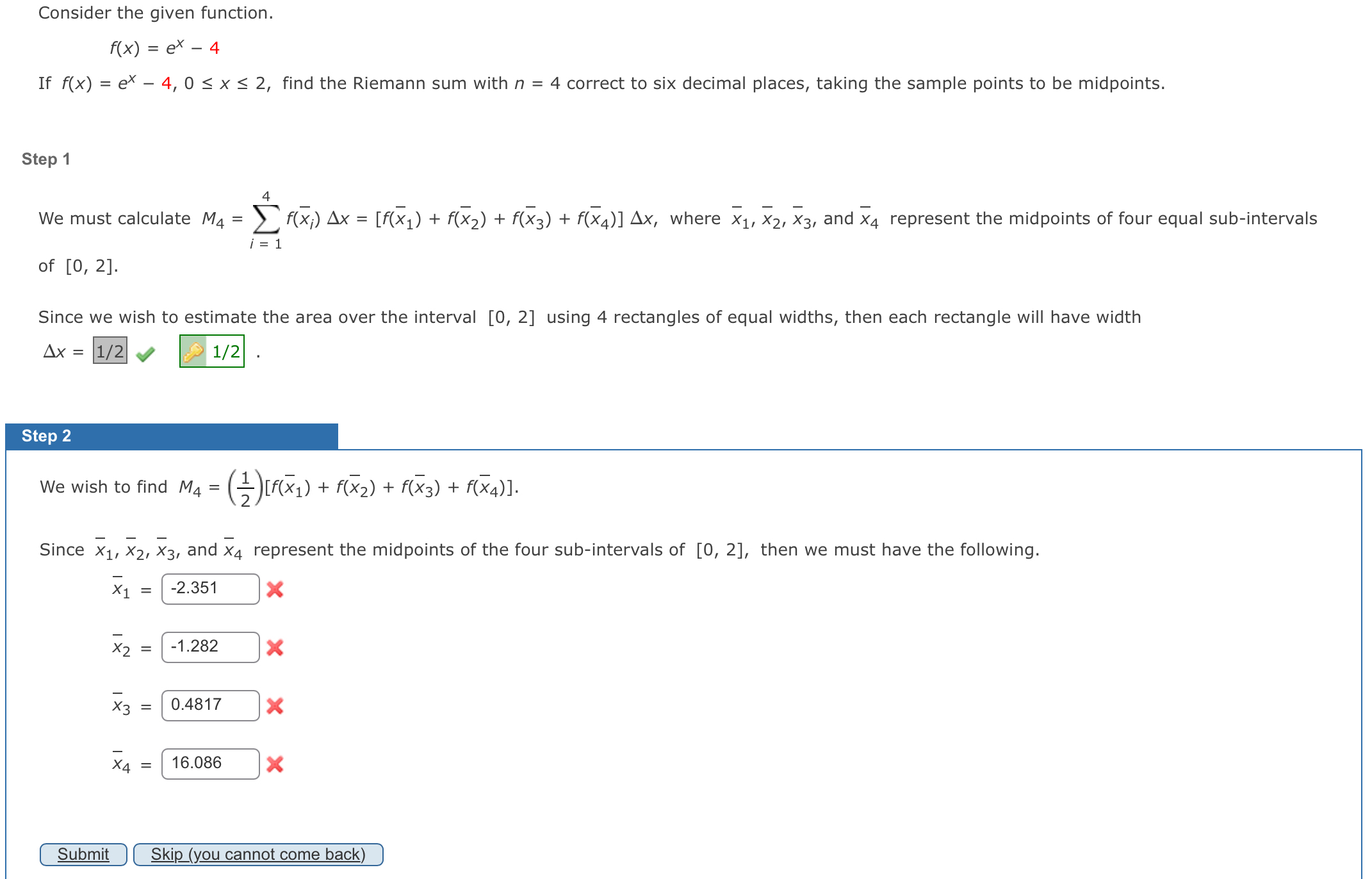
Consider the given function.

$f(x)=e^x-4$

If $f(x)=e^x-4,0x2,$ find the Riemann sum with $n=4$ correct to six decimal places, taking the sample points to be midpoints.

Step $1$

We must calculate $M_4={\displaystyle \underset{i=1}{\overset{4}{}}}f({\stackrel{}{x}}_i)x=[f({\stackrel{}{x}}_1)+f({\stackrel{}{x}}_2)+f({\stackrel{}{x}}_3)+f({\stackrel{}{x}}_4)]x,$ where ${\stackrel{}{x}}_1,{\stackrel{}{x}}_2,{\stackrel{}{x}}_3,$ and ${\stackrel{}{x}}_4$ represent the midpoints of four equal sub$-$intervals of $0,2.$

Since we wish to estimate the area over the interval $[0,2]$ using $4$ rectangles of equal widths, then each rectangle will have width

$x=\frac{1}{2}$

Step $2$

We wish to find $M_4=(\frac{1}{2})[f({\stackrel{}{x}}_1)+f({\stackrel{}{x}}_2)+f({\stackrel{}{x}}_3)+f({\stackrel{}{x}}_4)].$

Since ${\stackrel{}{x}}_1,{\stackrel{}{x}}_2,{\stackrel{}{x}}_3,$ and ${\stackrel{}{x}}_4$ represent the midpoints of the four sub$-$intervals of $0,2,$ then we must have the following.

${\stackrel{}{x}}_1=$

${\stackrel{}{x}}_2=-1\mathrm{.}282$

${\stackrel{}{x}}_3=$

${\stackrel{}{x}}_4=$