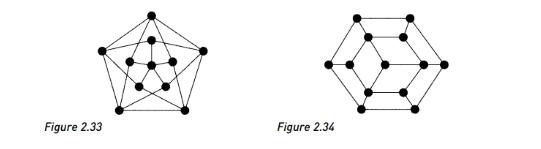
(i) Prove that, if G is a bipartite graph with an odd number of vertices, then G is non-Hamiltonian. (ii) Deduce that the graph in Fig. 2.34 is non-Hamiltonian. Use the result of Exercise 2.31(i) to show that a knight cannot visit all the squares of a 5 x 5 or 7 x 7 chessboard exactly once by knight's moves and return to its starting point. Can a knight visit all the squares of a 6 x 6 chessboard? Figure 2.33 Figure 2.34