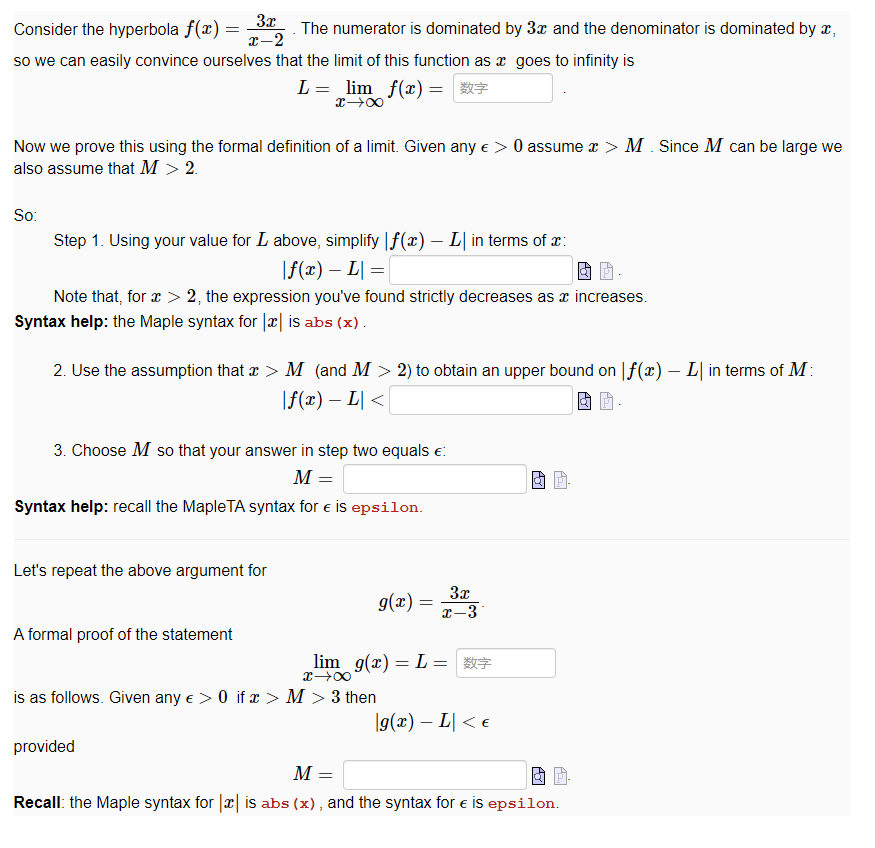
.

Consider the hyperbola f(x) = -2 The numerator is dominated by 3x and the denominator is dominated by c, so we can easily convince ourselves that the limit of this function as a goes to infinity is L = lim f(x) = = x-+00 Now we prove this using the formal definition of a limit. Given any 0 assume > > M . Since M can be large we also assume that M > 2. So: Step 1. Using your value for L above, simplify If(x) - L| in terms of &: If(x) - L| = Note that, for > > 2, the expression you've found strictly decreases as a increases. Syntax help: the Maple syntax for |x | is abs (x) . 2. Use the assumption that > > M (and M > 2) to obtain an upper bound on If(x) - L| in terms of M : If (2) - I 0 ifx > M > 3 then 19( x) - L|