Question: Consider the initial value problem, $$ (-1 x+4 y) y^{prime}=(x-8) sqrt{3}{y-8), yleft(x_{0} ight)=y_{0} $$ If $x_{0}=6$, then for what value of $y_{0}$ is a solution

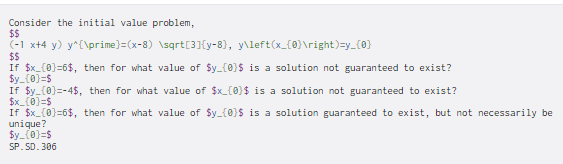
$Consider the initial value problem, $$ (-1 x+4 y) y^{\prime}=(x-8) \sqrt{3}{y-8),$

Consider the initial value problem, $$ (-1 x+4 y) y^{\prime}=(x-8) \sqrt{3}{y-8), y\left(x_{0} ight)=y_{0} $$ If $x_{0}=6$, then for what value of $y_{0}$ is a solution not guaranteed to exist? $y_{0}=$ If $y[0]=-4$, then for what value of $x_{0}$ is a solution not guaranteed to exist? $x_{0}=$ If $x_{0}=6$, then for what value of $y_{0}$ is a solution guaranteed to exist, but not necessarily be unique? $y_{0}=$ SP.SD. 306

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Prof. ll June 14, 2016 MAT224: Differential Equations Existence and Uniqueness of Solutions Consider the Initial Value Problem: y (x) = f (x, y) y(x0 ) = y0 . It would be good to know if a solution...

Consider the initial value problem, ( 9 x + 4 y ) y = ( x - 8 ) y - 2 3 , y ( x 0 ) = y 0 If x 0 = - 1 , then for what value of y 0 is a solution not guaranteed to exist? y 0 = If y 0 = - 2 , then...

The new line character is utilized solely as the last person in each message. On association with the server, a client can possibly (I) question the situation with a client by sending the client's...

10 Green's functions for PDEs In this final chapter we will apply the idea of Green's functions to PDEs, enabling us to solve the wave equation, diffusion equation and Laplace equation in unbounded...

Math 1152 Project #4 Solving Initial Value Problems using Power Series and the Laplace Transform Due: Tuesday, April 11 Name(s): - - - - - - - - - - - - - - - - - - - - Description - - - - - - - - -...

Consider the initial value problem for the function y , y ' - 3 c o s ( 3 t ) y 2 - 3 t 2 y 2 = 0 , y ( 0 ) = 1 ( a ) Find an implicit expression of all solutions y of the differential equation...

Please label each part. MA'l'll I-1l Homework 19 1.? 1. Consider the initial value problem {T} : augym) : 1. r :1: (a) Suppose the solution is given by y : on + 0.1.1? + (7.22:2 + $31173 + - - - for...

Can you please answer number 11 ONLY, I haven't been able to find it anywhere. I've uploaded the whole document for your reference just in case, but please let me know if there is anything else you...

Theorem 7.1. The fundamental existence theorem for ODE's. Consider the initial value problem z' = f(s, t), (to) = 10. Suppose f(t,) and (,) are both continuous on a region R containing the initial...

Should be done in Matlab please clear all defn = inline(-t*x,t,x); a=0; b=5; N=10; xa=1; h=(b-a)/N; t=a+h*(0:N); LT = length(t); x(1) = xa; for j=2:LT x(j) = x(j-1) + h*defn(t(j-1),x(j-1)); end...

The following selected transactions were completed by Chao Co. during May and June of the current year. The company sells to wholesalers and retail customers. The wholesalers resell the inventory....

Two research organizations rank countries by their economic competitiveness with quite different results. Based on these rankings address the following questions; ? Provide a brief overview of this...

10.79 The ratio of the students attending a mathematics exhibition from high school, higher secondary classes, undergraduate classes, and graduate classes is 3:5:6:2. Out of the 512 mathematics...

In how many different ways can Deeptha select her weekly conveyance schedule? 7 (2) 8 (3) 9 (4) None of these

10. Employee development is rewarded, which signals managers that mentoring and other development activities are worth their time and effort.

1. Mentor and protg participation is voluntary. Relationship can be ended at any time without fear of punishment.

5. Benefits of rotation are maximized and costs are minimized through timing the rotations to reduce work load costs and help employees understand the job rotations role in their development plans.