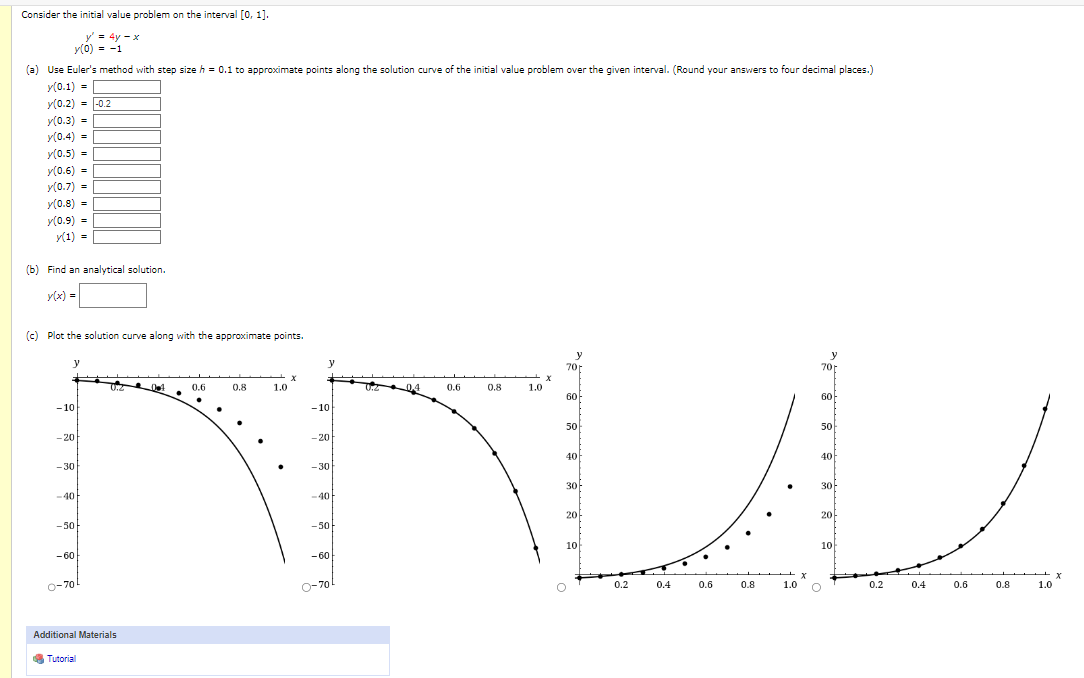
Question: Consider the initial value problem on the interval [0, 1]. y' = 4y - X (0) = -1 (0.1) = (a) Use Euler's method with
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


