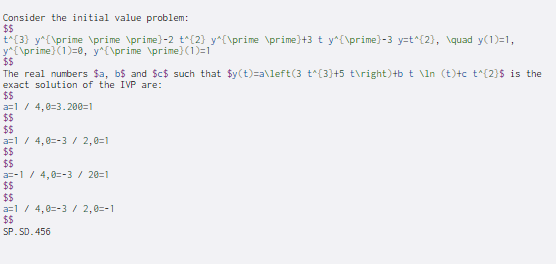
Consider the initial value problem: $$ t*{3}y"{\prime prime prime)-2 t^{2) y^{\prime \prime]+3 t y^{\prime)-3 y=t^{2}, \quad y(1)=1, y^{\prime) (1)=0, y^{\prime \prime} (1)=1 $$ The real numbers $a, b$ and $c$ such that $y(t)=a\left(3 t*{3}+5 t ight) +b t \ln (t)+c t^{2}5 is the exact solution of the IVP are: $$ a=1 / 4,2=3.200=1 $$ $$ a=1 / 4,8=-3 / 2,0=1 $$ $$ a=-1 / 4,5-3 / 20=1 $$ $$ a=1 / 4,0=-3 / 2,05-1 $$ SP.SD.456