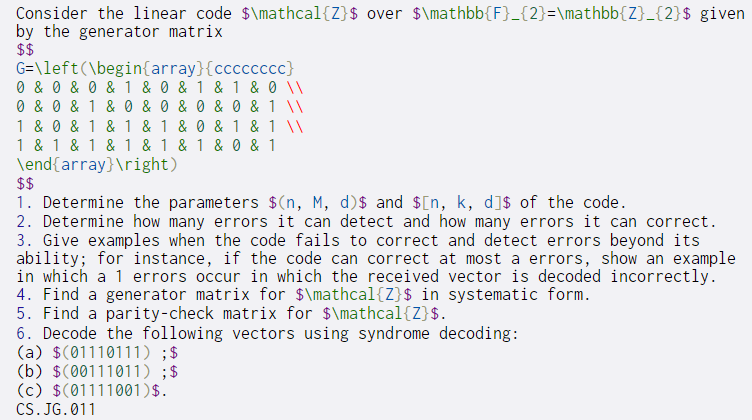
Consider the linear code $\mathcal{Z}$ over $\mathbb{F}_{2}=\mathbb{Z}_{2}$ given by the generator matrix $$ G=\left(\begin{array}{cccccccc} 0 & 0 & 0 & 1 & 0 & 1 & 1 & 0 0 & 0 & 1 & 0 & 0 & 0 & 0 & 11 1 & 0&1&1&1 & 0&1&1 W 1 & 1 & 1 & 1 & 1 & 1 & 0 & 1 \end{array} ight) $$ 1. Determine the parameters $(n, M, d)$ and $[n, k, d]$ of the code. 2. Determine how many errors it can detect and how many errors it can correct. 3. Give examples when the code fails to correct and detect errors beyond its ability; for instance, if the code can correct at most a errors, show an example in which a 1 errors occur in which the received vector is decoded incorrectly. 4. Find a generator matrix for $\mathcal{Z}$ in systematic form. 5. Find a parity-check matrix for $\mathcal{Z}$. 6. Decode the following vectors using syndrome decoding: (a) $C01110111) ;$ (b) $(00111011) ;$ (c) $(01111001) $. CS.JG.011