Consider the linear programming game example of Rock Paper Scissors. Suppose we have the following loss matrix for Player 1 (i.e. showing how much Player 1 loses rather than gains, so reverse the sign):

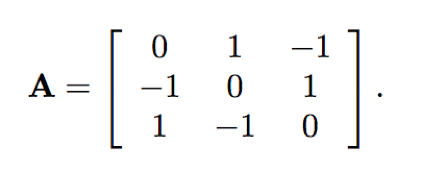
a. What is the expected loss for Player 1 when Player 1 plays a mixed strategy where x=(x_1,x_2,x_3) and Player 2 plays a mixed strategy of y=(y_1,y_2,y_3)?

b. Show that Player 1 can achieve a negative expected loss (i.e. an expected gain) if Player 2 plays any strategy other than y=(y_1,y_2,y_3)=(1/3,1/3,1/3).

c. Show that x=(1/3,1/3,1/3) and y=(1/3,1/3,1/3) form a Nash equilibrium.

d. Let x=(1/3,1/3,1/3) as in part c. Is it possible for (x,y) to be a Nash equilibrium for some mixed strategy y != (1/3,1/3,1/3)? Explain.

0 1 A=1-1 0 1 1 0 0 1 A=1-1 0 1 1 0