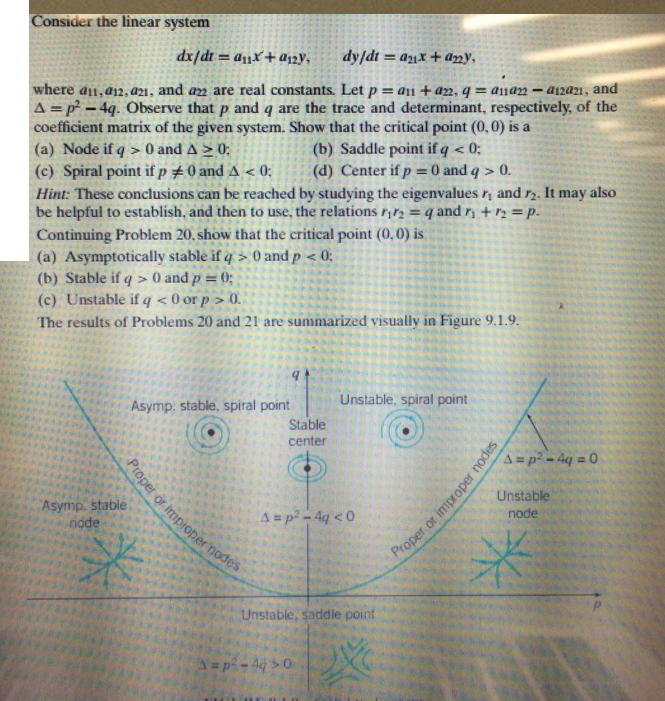
Consider the linear system dx/dt = ax + ay, dy/dt = anx+any. where an, a12, a21, and a22 are real constants. Let p = a1 + a2, q=anan-a12421, and A=p-4q. Observe that p and q are the trace and determinant, respectively, of the coefficient matrix of the given system. Show that the critical point (0,0) is a (a) Node if q> 0 and A > 0: (c) Spiral point if p = 0 and A < 0: Hint: These conclusions can be reached by studying the eigenvalues , and r2. It may also be helpful to establish, and then to use, the relations /2 = q and r + = p. Continuing Problem 20. show that the critical point (0,0) is (a) Asymptotically stable if q> 0 and p < 0: (b) Stable if q> 0 and p = 0; (c) Unstable if q 0. The results of Problems 20 and 21 are summarized visually in Figure 9.1.9. Asymp, stable, spiral point Proper or improper modes Asymp, stable. node (b) Saddle point if q < 0; (d) Center if p = 0 and q> 0. Stable center Unstable, spiral point A=p-4q 0 Unstable, saddle point roper or improper node A=p-4q=0 Unstable node *