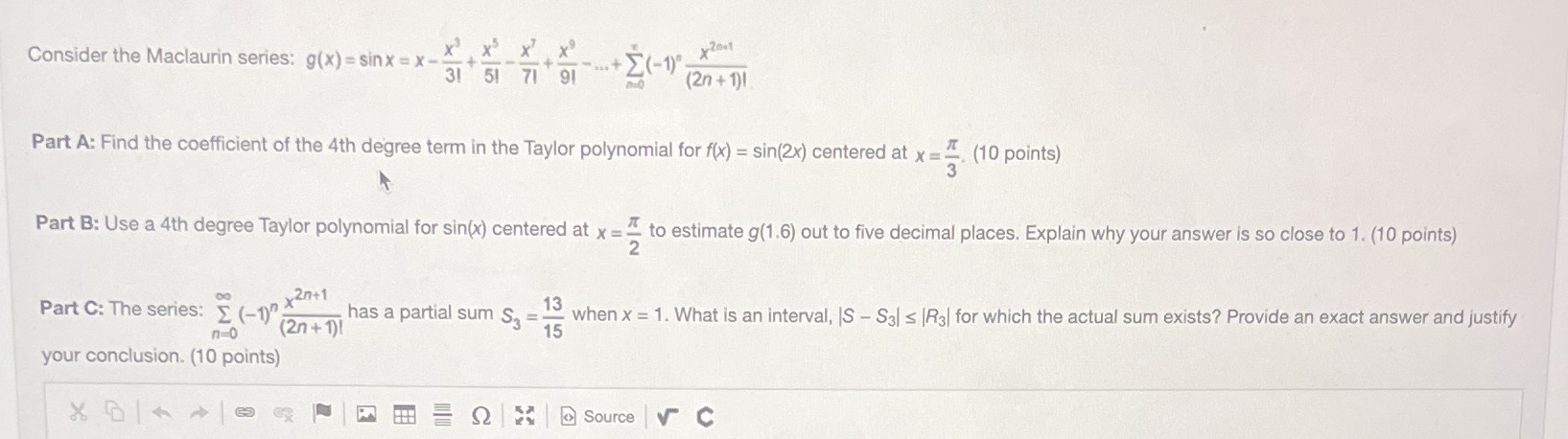
Consider the Maclaurin series: g(x) = sinx = x_ X x x' x x 20.1 31 51 71 91 -...+ E(-1)" (2n + 1)1 Part A: Find the coefficient of the 4th degree term in the Taylor polynomial for f(x) = sin(2x) centered at x = . (10 points) Part B: Use a 4th degree Taylor polynomial for sin(x) centered at x = - to estimate g(1.6) out to five decimal places. Explain why your answer is so close to 1. (10 points) Part C: The series: J (-no x20+1 (2n + 1 ) ! has a partial sum S, = " when x = 1. What is an interval, IS - Sal s |Ral for which the actual sum exists? Provide an exact answer and justify 15 your conclusion. (10 points) PA Q Source V C