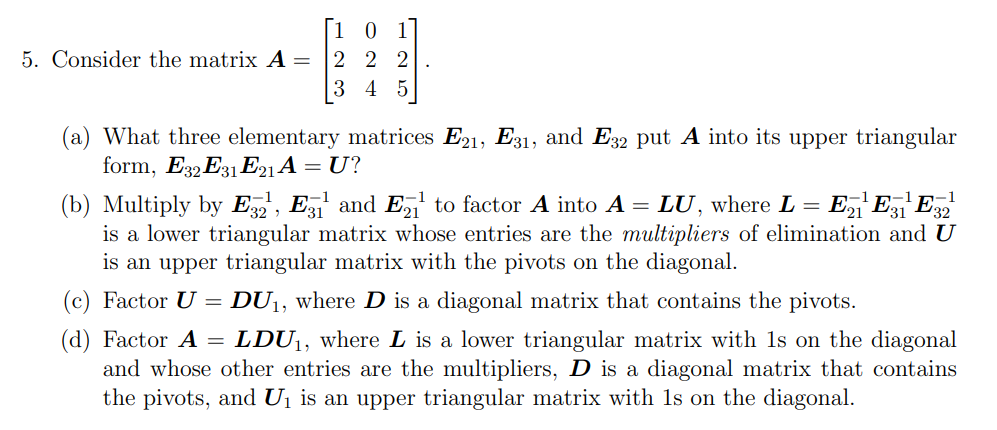
Consider the matrix A=123024125 (a) What three elementary matrices E21,E31, and E32 put A into its upper triangular form, E32E31E21A=U ? (b) Multiply by E321,E311 and E211 to factor A into A=LU, where L=E211E311E321 is a lower triangular matrix whose entries are the multipliers of elimination and U is an upper triangular matrix with the pivots on the diagonal. (c) Factor U=DU1, where D is a diagonal matrix that contains the pivots. (d) Factor A=LDU1, where L is a lower triangular matrix with 1s on the diagonal and whose other entries are the multipliers, D is a diagonal matrix that contains the pivots, and U1 is an upper triangular matrix with 1s on the diagonal