Question: Consider the model problem below, find A and R matrices, and b and r vectors. Then find the solution: -(xu'(x))' = 4x x EI
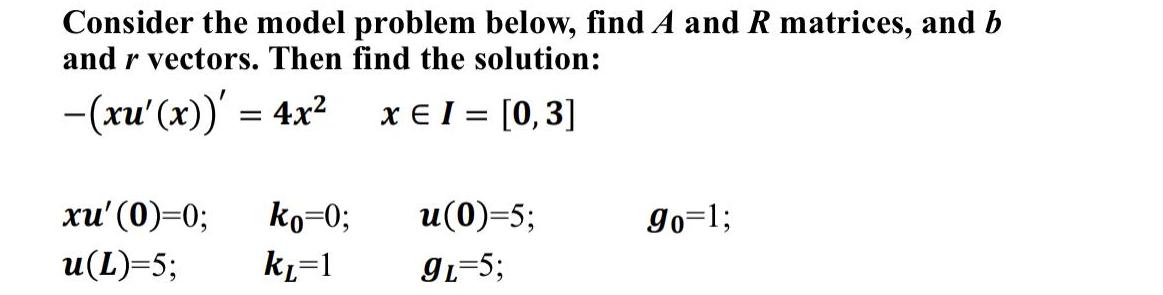

![= [0, 3] xu' (0)=0; u(L)=5; ko=0; k=1 u(0)=5; 9L=5; 90=1; Solve](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2022/10/633fe3d894cc4_1665131479551.jpg)
![the model problem below analytically -u"=f_1=[0,3]; u(0)=u(3)=0; for f(x)=5 f(x)=2x f(x)=x A](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2022/10/633fe3e75d6c0_1665131494815.jpg)
Consider the model problem below, find A and R matrices, and b and r vectors. Then find the solution: -(xu'(x))' = 4x x EI = [0, 3] xu' (0)=0; u(L)=5; ko=0; k=1 u(0)=5; 9L=5; 90=1; Solve the model problem below analytically -u"=f_1=[0,3]; u(0)=u(3)=0; for f(x)=5 f(x)=2x f(x)=x A model Problem with Variable Coefficients = 1ap dx aq? Aii = = [ aq? dx + Xi-1 = 1 aihi + ai+1 hi ai ai+1 " hi+1' - pxi+l Xi (-1) h+! (A+R)=b+r auf a -hi+l dx i=1,2,...,n-1 A+1 = [ av +19 | dx = ["' + a 1 + 19 idx pxi+1 1x ai +1 =- (-1) hi+l di+1 hi+1 . 1 hi+l = 0, 1,...,n -hi+l A model Problem with Variable Coefficients A + R = 4 -4 -44+%22 b+r= 515 $18 (A+R)=b+r E an-an-1 + hn-1 hn-1 f(xo)h1/2 f(x)(hi+h)/2 f(x2)(h2 +h3)/2 - : f(xn-1)(hn-1 + hn)/2 f(xn)hn/2 an hn + f hn an Kogo KLBL + Ko KL
Step by Step Solution
There are 3 Steps involved in it
To solve the given model problem we will first derive the A and R matrices as well as the b and r ve... View full answer

Get step-by-step solutions from verified subject matter experts


