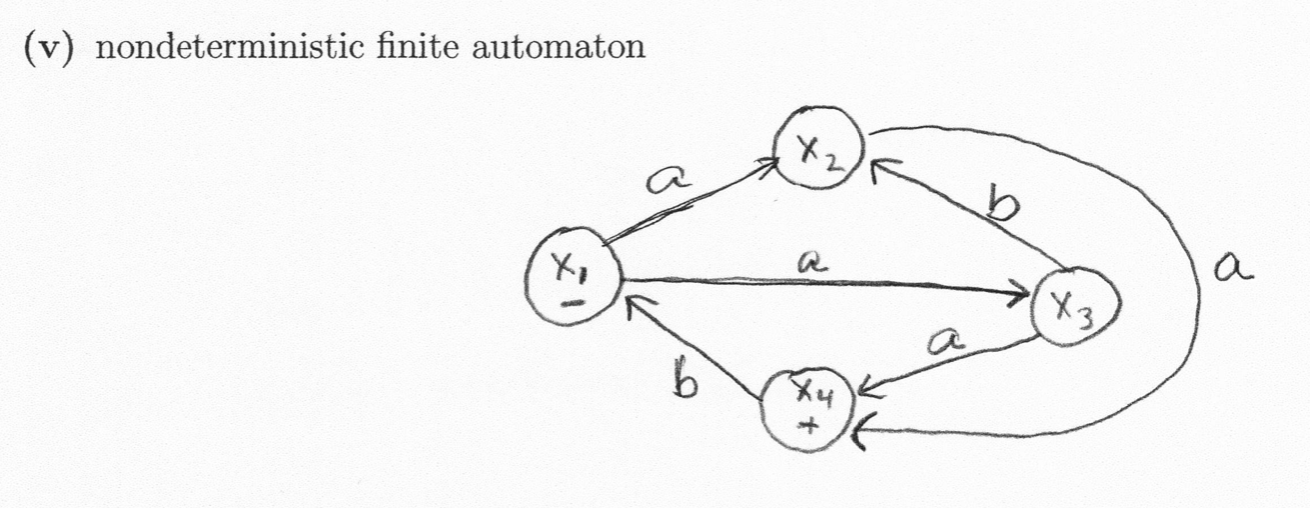Consider the NFA given above. Convert this NFA into an FA using the constructive algorithm presented in the Theorem below:

Theorem: Every language that can be defined by a nondeterministic finite automaton can also be defined by a deterministic finite automaton.

Proof (2): By constructive algorithm

Algorithm: nondeterministic automaton -> deterministic automaton (FA)

Given: a nondeterministic automaton whose states are {x1, x2, x3, ...}

1. For every subset of states, create a state of the new FA.
2. Make the transition table for all the new states (or just the new states that can be entered).
3. Add a state theta. Add transitions that loop back to itself for all letters of the alphabet. For each new state, if there is no transition for letter p, add one that goes to the theta state.
4. The final states must be those that contain at least one final state from the original nondeterministic finite automaton.
5. 

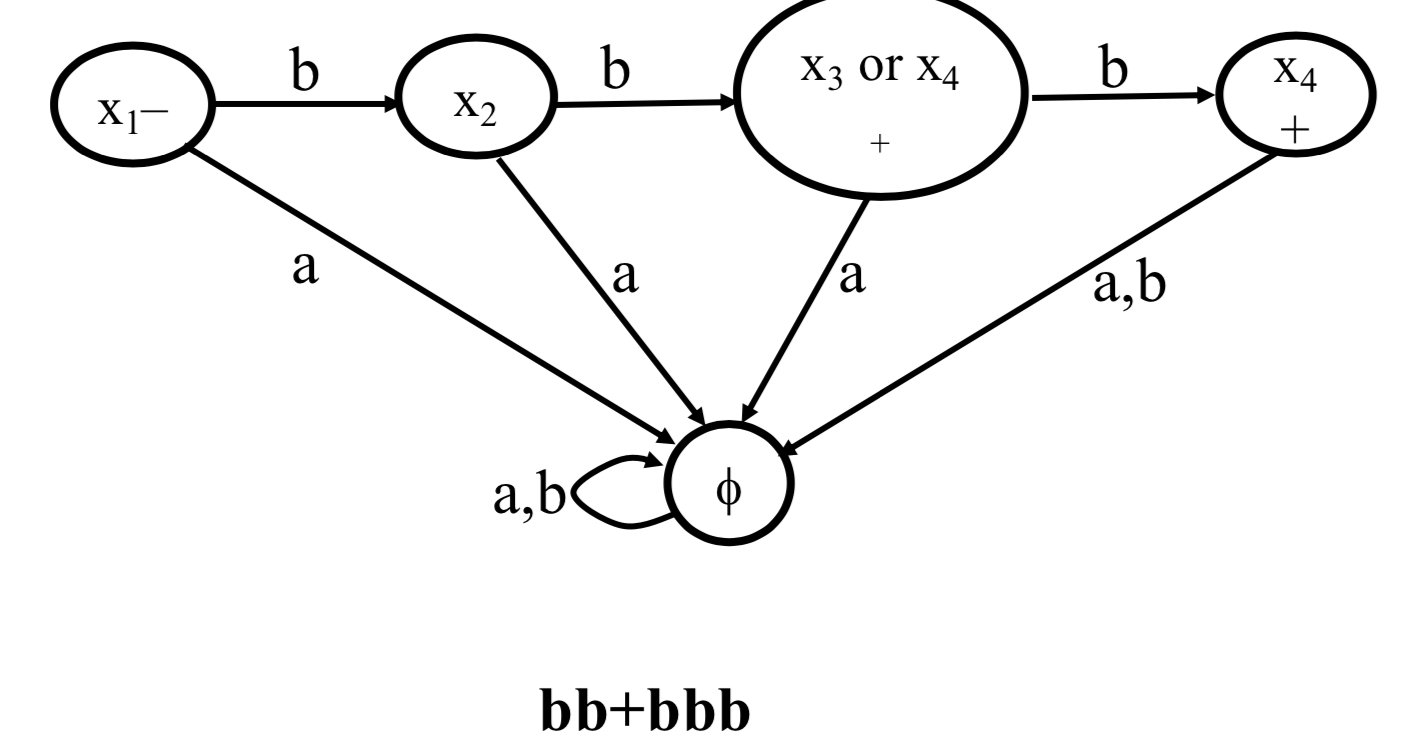
(v) nondeterministic finite automaton X3 or X4 X1 + ab a,bco bb+bbb