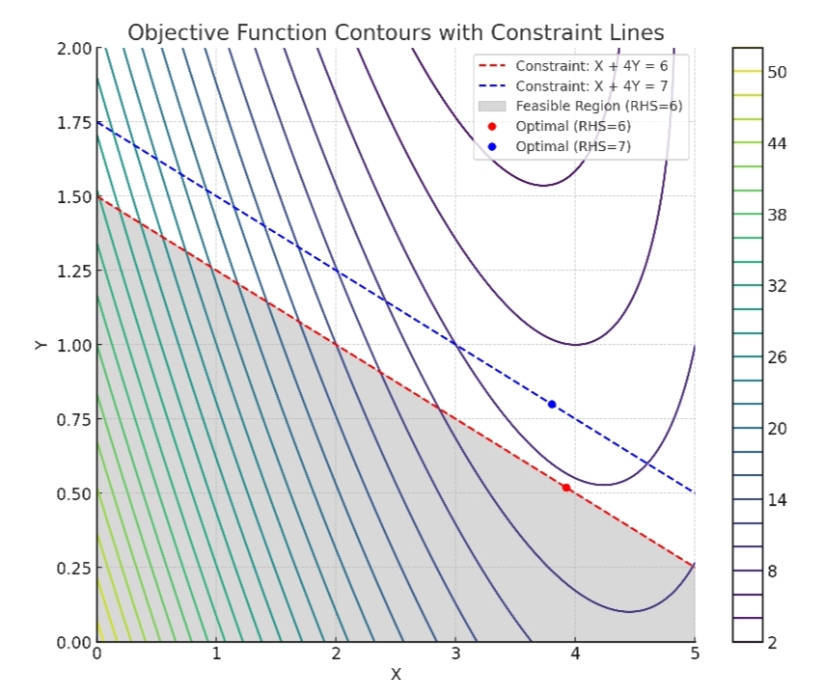
Question: Consider the nonlinear optimization model stated below.Min 2X2 ? 18X + 2XY + Y2 ? 14Y + 51s.t. X + 4Y ? 6(a)Find the minimum
Consider the nonlinear optimization model stated below.Min 2X2 ? 18X + 2XY + Y2 ? 14Y + 51s.t. X + 4Y ? 6(a)Find the minimum solution to this problem.32 Changed: Your submitted answer was incorrect. Your current answer has not been submitted. at (X, Y) = Incorrect: Your answer is incorrect. (b)If the right-hand side of the constraint is increased from 6 to 7, how much do you expect the objective function to change?Based on the dual value on the constraint X + 4Y ? 6, we expect the optimal objective function value to decrease by -8 Changed: Your submitted answer was incorrect. Your current answer has not been submitted. .(c)Resolve the problem with a new right-hand side of the constraint of 7. How does the actual change compare with your estimate?If we resolve the problem with a new right-hand-side of 7 the new optimal objective function value is 40 Incorrect: Your answer is incorrect. , so the actual change is a decrease of 3 Changed: Your submitted answer was incorrect. Your current answer has not been submitted. rather than what we expected in part (b).
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


