Question: Consider the ODE y - 2y + y = cos(4t). (a) Find the null solution yn (t). (b) Find a particular solution y, (t)

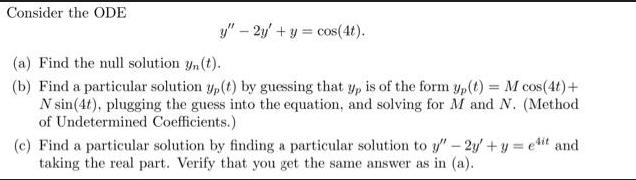
Consider the ODE y" - 2y + y = cos(4t). (a) Find

Consider the ODE y" - 2y + y = cos(4t). (a) Find the null solution yn (t). (b) Find a particular solution y, (t) by guessing that yp is of the form y(t) = M cos(4t) + N sin (4t), plugging the guess into the equation, and solving for M and N. (Method of Undetermined Coefficients.) (c) Find a particular solution by finding a particular solution to y" - 2y + y = eit and taking the real part. Verify that you get the same answer as in (a).

Step by Step Solution

★★★★★

3.45 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a To find the null solution we first solve the characteristic equation r2 2r 1 0 This factors as r12 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Planning is one of the most important management functions in any business. A front office managers first step in planning should involve determine the departments goals. Planning also includes...

In the floorlet Example 23.7, value the floorlet using risk- neutral valuation and show how you get the same answer as in the text.

On October 1 of the current year a corporation sold, at par plus accrued interest, $1,000,000 of its 12% bonds, which were dated July 1 of this year. What amount of bond interest expense should the...

Consider the null model, for simplicity with known ????2. After estimating ???? = E(y) by y, you plan to predict a future y from the N(????, ????2) distribution. State the formula for a 95%...

Recall the birthday application in Section 6.2.1. Imagine inspecting each of the r 2 pairs of people and noting whether both have the same birthday. (Ross, 1988, pp. 131 and 144(14)) (a) This is...

Reconsider the Leisure Airlines problem from Section 12.1. The demand forecasts shown in Table represent Leisure Airs best estimates of demand. But because demand cannot be forecasted perfectly, the...

Consider the two-dimensional solution space in Figure 3.17. (a) Suppose that the objective function is given as Maximize z = 6x1 + 3x2 If the simplex iterations start at point A, identify the path to...

Consider the null hypothesis H0: = 625. Suppose that a random sample of 29 observations is taken from a normally distributed population with = 32. Using a significance level of .01, show the...

Consider the null hypothesis H0: = 100. Suppose that a random sample of 35 observations is taken from this population to perform this test. Using a significance level of .01, show the rejection and...

Consider the null hypothesis H0: p = .65. Suppose a random sample of 1000 observations is taken to perform this test about the population proportion. Using = .05, show the rejection and...

Flight Caf prepares in-flight meals for airlines in its kitchen located next to a local airport. The companys planning budget for July appears below: Flight Caf Planning Budget For the Month Ended...

Our company makes and sells cell-phone sanitizer units. Cell phones are inserted inside the units and bathed in UV-C ultraviolet light that eliminates 99.9% of bacteria and viruses in approximately...

Suppose that a student suffering from migraine has a medical history that indicates the following probabilities. The probability that you will have a migraine in one day is 25%. If she has a migraine...

9. Your neighbor who has a job says, "I am having heart surgery in two months." When does your neighbor have to tell the employer about the surgery?

A group from the class in the previous question has identified a bug in their code that will take a minimum of 16 tasks T = {t1...t16} to resolve. How many ways are there to assign the tasks if (5...

During a heavy storm, lightning struck an office building that houses the data center of a small accounting firm. The lightning caused a fire that interrupted the electricity supply to the building...

A sold to B a tractor payable at P50,000 upon delivery and the balance of P70,000 within 60 days. B failed to take the delivery of the tractor and pay the purchase price. A was forced to sell the...

The maximum pressure that can be developed for a certain fluid power cylinder is 15.0 MPa. Compute the required diameter for the piston if the cylinder must exert a force of 30 kN.

Since its inception in 1967, the Super Bowl is one of the most watched events on television in the United States every year. The number of U.S. households that tuned in for each Super Bowl, reported...

Manning Autos operates an automotive service. To complete their repair work, Manning mechanics often need to retrieve parts from the company's parts department counter. Mechanics arrive at the parts...

The Burger Dome waiting line model in Section 11.1 studies the waiting time of customers at its fast-food restaurant. Burger Dome's single-server waiting line system has an arrival rate of 0.75...

=+a. What is the purpose of measuring efficiency every 100 miles? Why not just measure efficiency at the end of the 500-mile course?

=+21. A researcher wants to test the effectiveness of a new fuel additive for increasing the fuel efficiency (miles per gallon, mpg) of automobiles. The researcher

=+proposes that a car be driven for a total of 500 miles and that at the end of each 100-mile segment the fuel efficiency be measured and recorded.