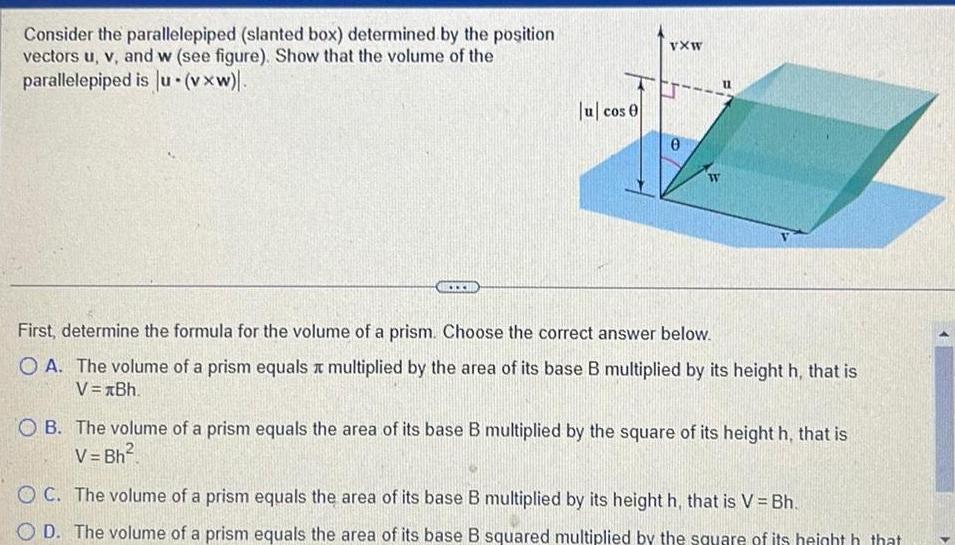
Consider the parallelepiped (slanted box) determined by the position vectors u, v, and w (see figure). Show that the volume of the parallelepiped is lu (vxw). lucose vxw W First, determine the formula for the volume of a prism. Choose the correct answer below. OA. The volume of a prism equals multiplied by the area of its base B multiplied by its height h, that is V=Bh. OB. The volume of a prism equals the area of its base B multiplied by the square of its height h, that is V=Bh2 OC. The volume of a prism equals the area of its base B multiplied by its height h, that is V = Bh. OD. The volume of a prism equals the area of its base B squared multiplied by the square of its heighth that