Consider the periodic function f(t) depicted in Figure 1. This periodic function repeats forever in the t and -t directions

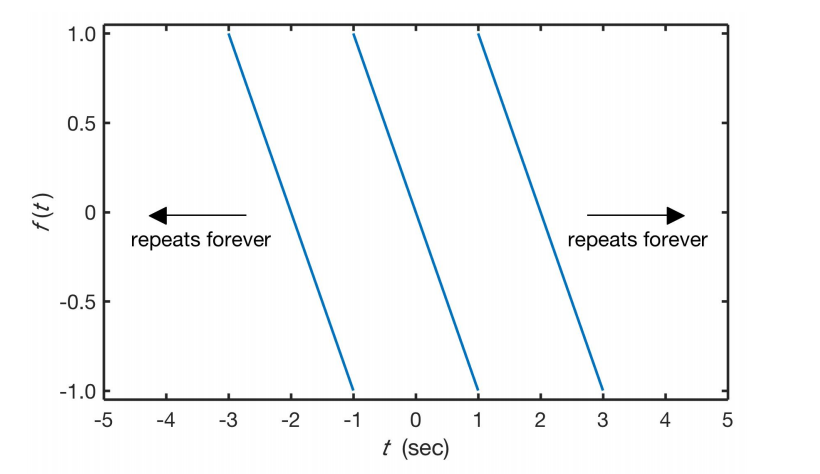Figure 1. The periodic function f(t).

Over the range -3 t -1, f(t) = -t - 2, over the range -1 t 1, f(t) = -t, over the range 1 t 3, f(t) = -t + 2, and so forth.

a. What is the period of the function shown in Figure 1?

b. Determine a combination of sine and cosine functions, that, when added, equal f(t). In other words, determine the Fourier series for f(t). Hint: use the sine/cosine Fourier series, not the complex exponential Fourier series.

c. Plot the first five terms (individual sine/cosine functions corresponding to n = 1, 2, 3, 4, and 5) of the Fourier series on the same plot using MatLab.

d. On a separate plot, show the sum of the first 20 terms of the Fourier series. How does your 20-term Fourier series approximation compare to f(t)? What about the first 400 terms?

1.0 F 0.5 repeats forever repeats forever 0.5 1.0E -5 -4 3 -21 0 23 4 5 t (sec)