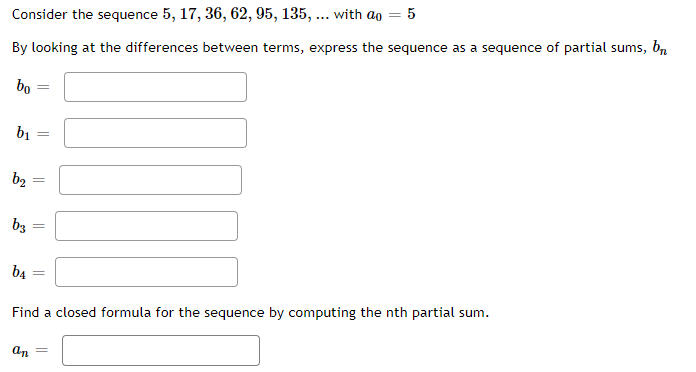
Consider the sequence 5, 17, 36, 62, 95, 135, ... with a = 5 By looking at the differences between terms, express the sequence as a sequence of partial sums, br bo b b b3 b = an = || = = Find a closed formula for the sequence by computing the nth partial sum. = Starting with any rectangle, we can create a new, larger rectangle by attaching a square to the longer side. For example, if we start with a 2 x 5 rectangle, we would glue on a 5 x 5 square, forming a 5 x 7 rectangle: The next rectangle would be formed by attaching a 7 x 7 square to the top or bottom of the 5 x 7 rectangle. a. Create a sequence of rectangles using the rule starting with a 1 x 2 rectangle. Then write out the sequence of perimeters for the rectangles (the first term of the sequence would be 6, since the perimeter of a 1 x 2 rectangle is 6 - the next term would be 10). Call this sequence an. a = a= a3 as = b. Repeat the above part starting with a 1 x 3 rectangle. Call the sequence of the perimeters of these rectangles bn. b b b3 b || = c. Find recursive formulas for each of the sequences of perimeters you found in parts a) and b). Don't forget to give the initial conditions as well. (Select the variable names from the Vars menu.) = an = b a= bo a = = = b Select an answer neither geometric arithmetic d. The sequences are Select an answer