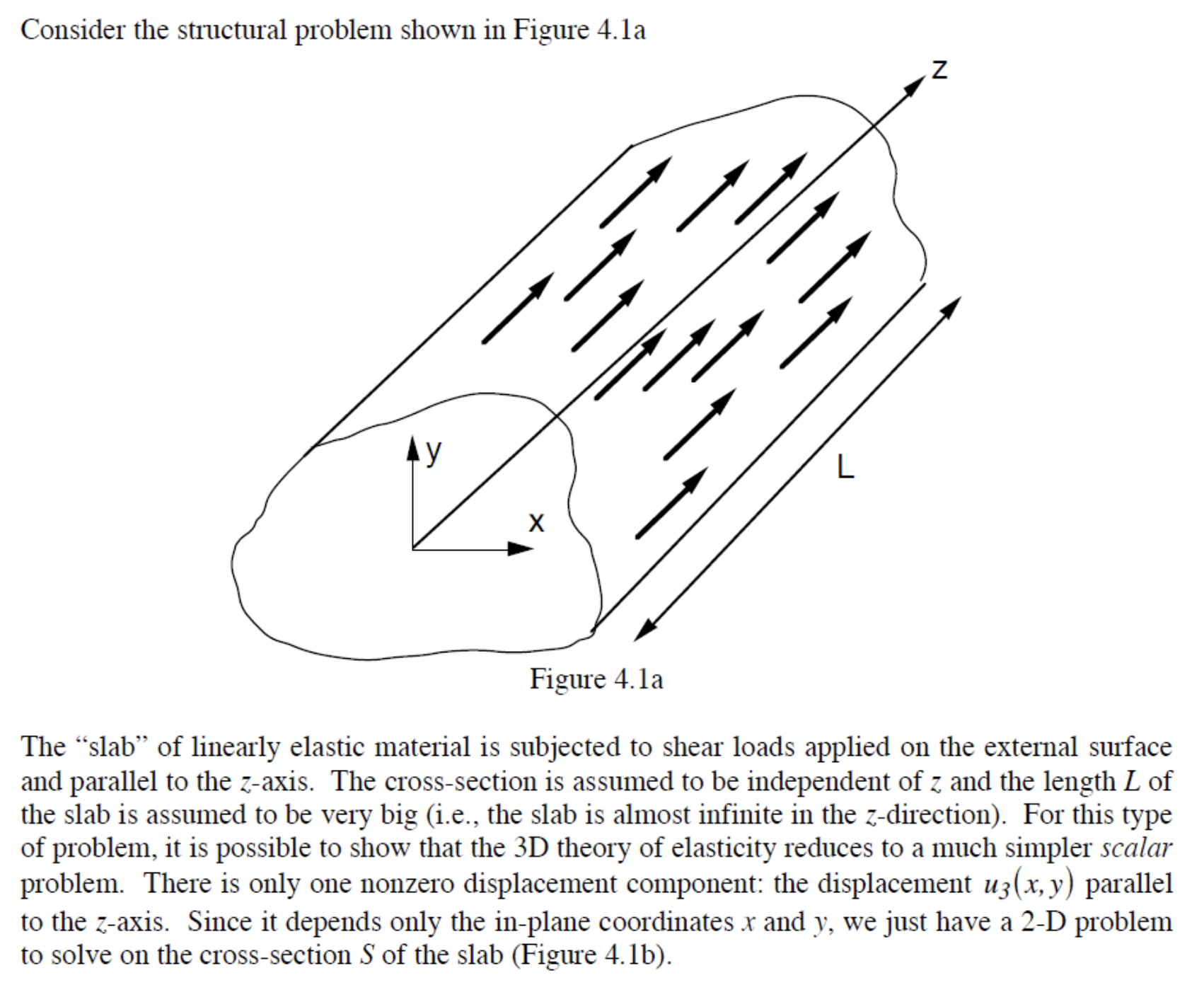
Consider the structural problem shown in Figure 4.1a y X L N Figure 4.1a The "slab" of linearly elastic material is subjected to shear loads applied on the external surface and parallel to the z-axis. The cross-section is assumed to be independent of z and the length L of the slab is assumed to be very big (i.e., the slab is almost infinite in the z-direction). For this type of problem, it is possible to show that the 3D theory of elasticity reduces to a much simpler scalar problem. There is only one nonzero displacement component: the displacement u3(x, y) parallel to the z-axis. Since it depends only the in-plane coordinates x and y, we just have a 2-D problem to solve on the cross-section S of the slab (Figure 4.1b). u Figure 4.1b The displacement u(x, y) (which is perpendicular to the plane of the cross-section) can be shown to satisfy the following scalar equation Fuz dx 13 * uz = uz along Tu (imposed displacement), Juz In 013 + dy where u denotes the shear modulus and f3 is the (distributed) body force parallel to the z-axis. We have two types of boundary conditions = d uz\ = * + f3(x,y)= 0 on S, II = S * where u3 and T3 denote the applied (and therefore known) out-of-plane displacement and traction, respectively, and n is the outward normal to the boundary. = T3 along IT (imposed traction), For this class of problems (called anti-plane shear problems), there are only two non-zero stress and strain components 1 2 dx 213, 023 23 = y 1 duz 2 dy X 2 23.. r The potential energy II for anti-plane shear problems is given by - 75 (013 13 + 023 23) dS Sf3 uz ds S S - * ST3 uz dIT. IT Using the PMPE approach, derive the finite element formulation (i.e., local stiffness matrix and local load vector) for a generic (global) M-node 2-D anti-plane shear element. Provide your solution in both vector and component forms. Make sure to provide comments on every step of the derivation.