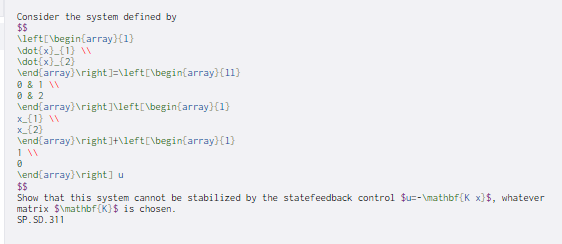
Consider the system defined by $$ \left\begin{array}{1} \dot{x}_{1} \dot{x}_{2) \end{array} ight)=\left\begin{array}11) & 1 0 & 2 \end{array} ight]\left\begin{array}{1} x_{1} x_{2) \end{array} ight]+\left|\begin{array}{l) 1 \end{array} ight] u $$ Show that this system cannot be stabilized by the statefeedback control $u=-\mathbf {K x}$, whatever matrix $\mathbf {k}$ is chosen. SP.SD.311