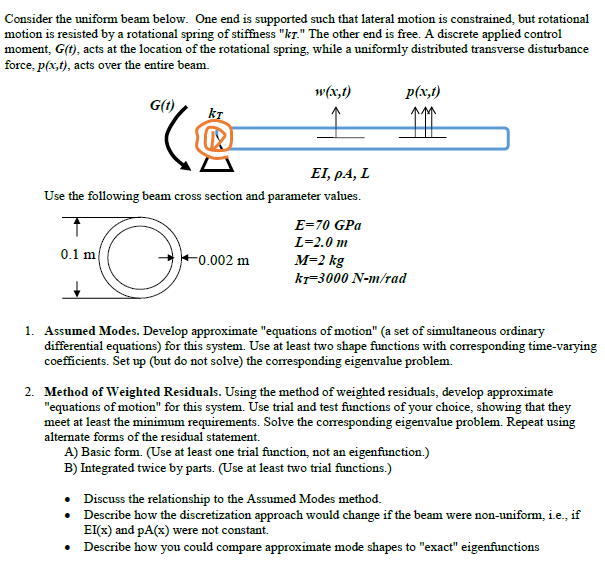
Consider the uniform beam below. One end is supported such that lateral motion is constrained, but rotational motion is resisted by a rotational spring of stiffness "kt." The other end is free. A discrete applied control moment, G(t), acts at the location of the rotational spring, while a uniformly distributed transverse disturbance force, p(x,t), acts over the entire beam. w(x,t) p(x,1) G() ki EI, P4, L Use the following beam cross section and parameter values. E=70 GPa L=2.0 m 0.1 m +0.002 m M=2 kg kr=3000 N-m/rad -o 1. Assumed Modes. Develop approximate "equations of motion" (a set of simultaneous ordinary differential equations) for this system. Use at least two shape functions with corresponding time-varying coefficients. Set up (but do not solve the corresponding eigenvalue problem. 2. Method of Weighted Residuals. Using the method of weighted residuals, develop approximate "equations of motion for this system. Use trial and test functions of your choice, showing that they meet at least the minimum requirements. Solve the corresponding eigenvalue problem. Repeat using alternate forms of the residual statement. A) Basic form. (Use at least one trial function, not an eigenfunction.) B) Integrated twice by parts. Use at least two trial functions.) Discuss the relationship to the Assumed Modes method. Describe how the discretization approach would change if the beam were non-uniform, i.e., if EI(x) and pA(x) were not constant. Describe how you could compare approximate mode shapes to "exact" eigenfunctions Consider the uniform beam below. One end is supported such that lateral motion is constrained, but rotational motion is resisted by a rotational spring of stiffness "kt." The other end is free. A discrete applied control moment, G(t), acts at the location of the rotational spring, while a uniformly distributed transverse disturbance force, p(x,t), acts over the entire beam. w(x,t) p(x,1) G() ki EI, P4, L Use the following beam cross section and parameter values. E=70 GPa L=2.0 m 0.1 m +0.002 m M=2 kg kr=3000 N-m/rad -o 1. Assumed Modes. Develop approximate "equations of motion" (a set of simultaneous ordinary differential equations) for this system. Use at least two shape functions with corresponding time-varying coefficients. Set up (but do not solve the corresponding eigenvalue problem. 2. Method of Weighted Residuals. Using the method of weighted residuals, develop approximate "equations of motion for this system. Use trial and test functions of your choice, showing that they meet at least the minimum requirements. Solve the corresponding eigenvalue problem. Repeat using alternate forms of the residual statement. A) Basic form. (Use at least one trial function, not an eigenfunction.) B) Integrated twice by parts. Use at least two trial functions.) Discuss the relationship to the Assumed Modes method. Describe how the discretization approach would change if the beam were non-uniform, i.e., if EI(x) and pA(x) were not constant. Describe how you could compare approximate mode shapes to "exact" eigenfunctions