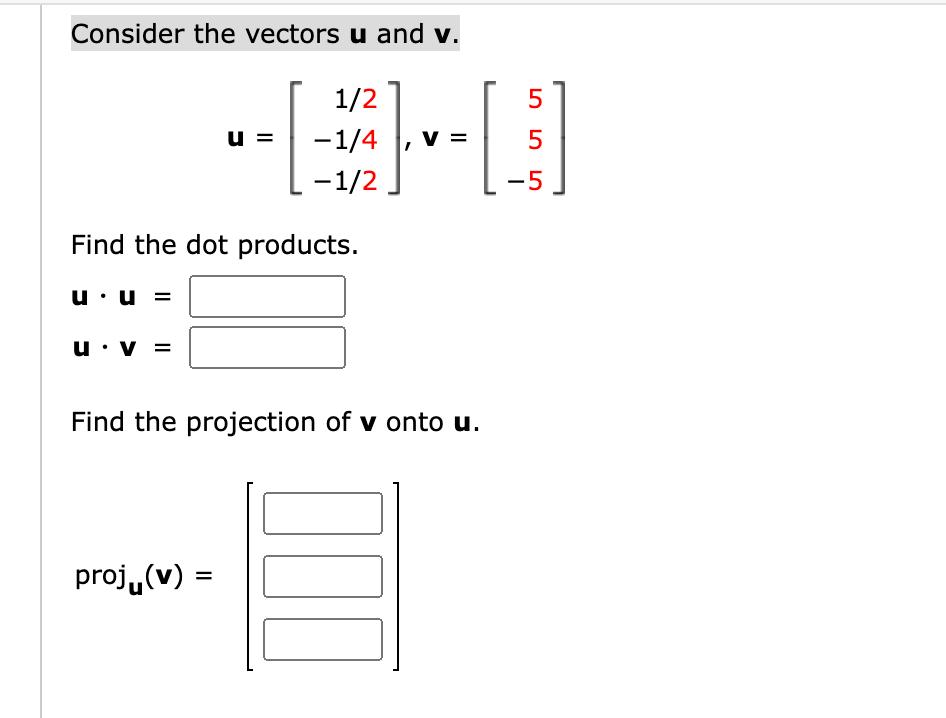
Question: Consider the vectors u and v. u Find the dot products. u. V U= 1/2 - 1/4 -1/2 proj(v) = Find the projection of

$Consider the vectors $ \mathbf{u} $ and $ \mathbf{v} $. \[ \mathbf{u}=\left[\begin{array}{r} 1 / 2 \\ -1 / 4 \\ -1 / 2 \e$

$Find all values of the scalar $ k $ for which the two vectors are orthogonal. (Enter your answers as a comma-separated list$

$Give the vector equation of the line passing through $ P $ and $ Q $. \[ P=(0,1,-1), Q=(-6,1,2) \] \[ \mathbf{x}=\left[\b$

Consider the vectors u and v. u Find the dot products. u. V U= 1/2 - 1/4 -1/2 proj(v) = Find the projection of v onto u. 5 5 -5 - Find all values of the scalar k for which the two vectors are orthogonal. (Enter your answers as a comma-separated list.) 2 [3], v = [K+1 k = U= Need Help? Submit Answer Read It Give the vector equation of the line passing through P and Q. P = (0, 1, 1), Q = (-6, 1, 2) X = 0 1 -1 - + t 000

Step by Step Solution

★★★★★

3.42 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Solve the equation by using an LUP decomposition. 15 4 2 0 3 X1 12 X2 5 8 2 X3 5

1. The ________ ________ of two vectors yields a scalar, rather than a vector. 2. The dot product of u = (u1, u2) and v = (v1, v2) is u v = ________. 3. If is the angle between two nonzero vectors...

1. What can be said about the vectors u and v under each condition? (a) The projection of u onto v equals u. (b) The projection of u onto v equals 0. 2. Proof Use vectors to prove that the diagonals...

Find an equation for the plane spanned by the vectors u = (-1, 1, 1) and v = (3, 4, 4).

Compute the dot product of the vectors u and v, and find the angle between the vectors. u (3,-5, 2) and v = (-9,5, 1)

Compute the dot product of the vectors u and v, and find the angle between the vectors. = i and v = i + V3j u =

In Problems 1924, use the method of Example 3 to determine whether the given vectors u, v, and w are linearly independent or dependent. If they are linearly dependent, find scalars a, b, and c not...

Given the vectors u = (1, 0, 0), v = (1, 1, 0), w = (1, 1, 1) and s = (2, 1, 2), find , , that satisfy s = u + v + w. If u = (1, 1, 0), v = (0, 1, 1) and w = (0, 0, 1) show that

24.3. Asymmetric well potential It is interesting to see what happens when the bosonic potential has two asymmetric wells | a and | b: in this case the asymptotic behaviours of the kink at xare...

A.3. Consider the subset of R4 given by X = {(2, 2, 1, 3), (7, 5, 5, 5), (3, 2, 2, 1), (2, 1, 2, 1)}. Find a basis of Span X and extend this to a basis of R4.

5. Solve the following difference equation: 2yn+2 - 3yn+1- 2y, = 1 Yo = 1, Y1 = 2 %3D %3D %3D

what is the most effective approach to developing a comprehensive global talent management strategy?

Prepare journal entries for each transaction. Post each of the journal entries to related T-accounts. Prepare a trial balance at the end of the month. Prepare any necessary adjusting entries. Prepare...

Palin's Muffler Shop has one standard muffler that fits a large variety of cars. The shop wishes to establish a periodic review system to manage inventory of this standard muffler. To determine the...

A. Circle the correct word(s). In some cases, both wordds are correct. The new pizzeria is (1. extremely / completely) popular. It's a (2. really /very) greet place to spend the evening with friends....

HAPPY SCAPE ADVERTISING Michael Mathers, Director at Happy scape Dianne Johnson, Finance officer at Happy scape Happy scape is a small advertising- printing business located in Cascade Peak. Happy...

Could you please use this data to find the difference between the R max and the one in the experiment data?

if a rectangle has sides of 1/4 and 2/3. What is a possible side length of a unit square that could be used to title the rectangle? 1/3,1/4,1/6, or 1/12

The exponential function y = ax for a = 0.5, 1.2, and 2.0. Which of these curves intersects the line y = x? Determine all positive numbers a for which the curve y = ax intersects the line y = x.

A driver's average speed is 50 miles per hour on a round trip between two cities 100 miles apart. The average speeds for going and returning were x and y miles per hour, respectively. (a) Show that y...

The pH of a solution decreases by one unit. By what factor does the hydrogen ion concentration increase? Use the acidity model pH log[H+], where acidity (pH) is a measure of the hydrogen ion...

2. Explain the breadth of research evidence for the universality of basic emotions.

In the first, photographs of facial expressions of emotion thought to portray universally recognizable emotions were shown to observers in different countries who had to label each expression. If the...

The potential for chaos is also great because of the very large individual differences that exist in any society.