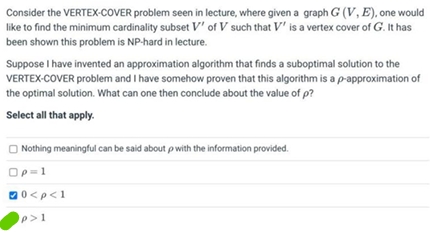
Consider the VERTEX$-$COVER problem seen in lecture, where given a graph $G(V,E),$ one would

like to find the minimum cardinality subset $V^{\text{'}}$ of $V$ such that $V^{\text{'}}$ is a vertex cover of $G.$ It has

been shown this problem is NP$-$hard in lecture.

Suppose I have invented an approximation algorithm that finds a suboptimal solution to the

VERTEX$-$COVER problem and I have somehow proven that this algorithm is a $-$approximation of

the optimal solution. What can one then conclude about the value of $?$

Select all that apply.

Nothing meaningful can be said about $$ with the information provided.

$=1$

$>1$