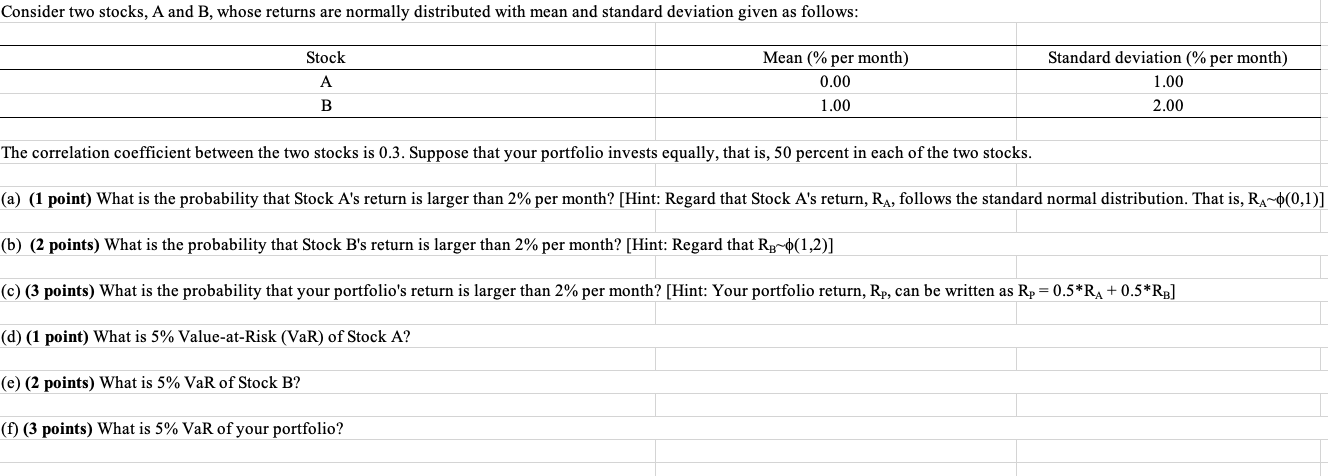
Consider two stocks, A and B, whose returns are normally distributed with mean and standard deviation given as follows: Stock A B Mean (% per month) 0.00 1.00 Standard deviation (% per month) 1.00 2.00 The correlation coefficient between the two stocks is 0.3. Suppose that your portfolio invests equally, that is, 50 percent in each of the two stocks. (a) (1 point) What is the probability that Stock A's return is larger than 2% per month? [Hint: Regard that Stock A's return, RA, follows the standard normal distribution. That is, RA~(0,1)] (b) (2 points) What is the probability that Stock B's return is larger than 2% per month? [Hint: Regard that RB~(1,2)] (c) (3 points) What is the probability that your portfolio's return is larger than 2% per month? [Hint: Your portfolio return, Rp, can be written as R = 0.5*RA + 0.5*RB] (d) (1 point) What is 5% Value-at-Risk (VaR) of Stock A? (e) (2 points) What is 5% VaR of Stock B? (f) (3 points) What is 5% VaR of your portfolio?