Considerer: 'A'=1, 'B"=2, 'C'=3, 'D'=4 and 'D'=5. sequebcie start an finish: NULL.

I did a matlab functions and are not running. Please could check, see below ( all function are in one only arquive).

%%HMM function [alpha] = fwd_alg(a,b,V) %alpha = fwd_alg(a,b,V) % %Inicia HMM foward

%a=matrix probabilidade transio estado %b=matrix prob. obser. %V=Sequenc. de Obs. T=length(V); Nhid = size(a,1); %inicializa alfa, %tempo zero = estado inicial = null

alpha=zeros(Nhid,T); alpha(1,1)=1; %calcula alpha for t=1:T-1 for j=1:Nhid alpha(j,t+1)=alpha(:,t)'*a(:,j)*b(j,V(t+1)); end end %% function [beta] = bkwd_alg(a,b,V) %beta = bkwd_alg(a,b,V) %Inicia HMM backward

%a=matrix probabilidade transio estado %b=matrix prob. obser. %V=Sequenc. de Obs. T=length(V); Nhid = size(a,1); %inicializa Beta, %tempo zero = estado inicial = null

beta=zeros(Nhid,T); beta(:,T)=1; %calcula beta for t=T-1:-1:1 for i=1:Nhid beta(i,t)=sum(a(i,:)'.*beta(:,t+1).*b(:,V(t+1))); end end %% function [alpha,beta,gamma,xi]=fwd_bkwd(a,b,V) %[alpha, beta,gamma,xi]=fwd_bkwd(a,b,V) [alpha]=fwd_alg(a,b,V); beta=bkwd_alg(a,b,V); Nhid=size(a,1); T=length(V); %% %Calculo de Gama gamma=zeros(Nhid,T); for t=1:T for i=1:Nhid gamma(i,t)=alpha(i,t)*beta(i,t); end gamma(:,t)=gamma(:,t)/sum(gamma(:,t)); end xi=zeros(Nhid,Nhid,T-1); for t=1:T-1 for i=1:Nhid for j=1:Nhid xi(i,j,t)=alpha(i,t)*a(i,j)*... b(j,V(t+1))*beta(j,t+1); end end xi(:,:,t)=xi(:,:,t)/sum(sum(xi(:,:,t))); end %end function [alpha,beta,gamma,xi]=fwd_bkwd(a,b,V) %[alpha, beta,gamma,xi]=fwd_bkwd(a,b,V) [alpha]=fwd_alg(a,b,V); beta=bkwd_alg(a,b,V); Nhid=size(a,1); T=length(V); %% %Calculo de Gama gamma=zeros(Nhid,T); for t=1:T for i=1:Nhid gamma(i,t)=alpha(i,t)*beta(i,t); end gamma(:,t)=gamma(:,t)/sum(gamma(:,t)); end xi=zeros(Nhid,Nhid,T-1); for t=1:T-1 for i=1:Nhid for j=1:Nhid xi(i,j,t)=alpha(i,t)*a(i,j)*... b(j,V(t+1))*beta(j,t+1); end end xi(:,:,t)=xi(:,:,t)/sum(sum(xi(:,:,t))); end %end %% function [a,b]=train(V,Nhid,Nvis) %[a,b]=train(V,Nhid,Nvis) % %Dado uma sequencia de obs, treine a HMM %V=sequenca de observaes Nseq=length(V); %inicializando a trans estado a=ones(Nhid,Nhid)/(Nhid-1); a(Nhid,:)=0; a(:,1)=0; a(Nhid,Nhid)=1; % % for i=1:Nhid-1 for j=2:Nhid a(i,j)=a(i,j)+randn*1e-2; end end %% %Inic. prob matrix b=ones(Nhid,Nvis)/(Nvis-1); b(1,:)=0; b(Nhid,:)=0; b(:,Nvis)=0; b(1,Nvis)=1; b(Nhid,Nvis)=1; % %treinando com a sequencia % delta_max=inf; delta_thresh=1e-3; numiter=0; while delta_max>delta_thresh a0=a; b0=b; for s=1:Nseq %calcula alpha,beta, gamma e xi [alpha,beta,gamma,xi]=fwd_bkwd(a,b,V{s}); Gamma{s}=gamma; Xi{s}=xi; end % atualiza matrizes a e b [a,b]=update(a,b,Gamma,Xi,V); %verificao de convergncia delta_a=max(max(abs(a-a0))); delta_b=max(max(abs(b-b0))); delta_max=max(delta_a,delta_b); numiter=numiter+1; end fprintf('treinado com %d interacoes ',numiter) %% function [a,b]=train(V,Nhid,Nvis) %[a,b]=train(V,Nhid,Nvis) % %Dado uma sequencia de obs, treine a HMM %V=sequenca de observaes Nseq=length(V); %inicializando a trans estado a=ones(Nhid,Nhid)/(Nhid-1); a(Nhid,:)=0; a(:,1)=0; a(Nhid,Nhid)=1; % % for i=1:Nhid-1 for j=2:Nhid a(i,j)=a(i,j)+randn*1e-2; end end %% %Inic. prob matrix b=ones(Nhid,Nvis)/(Nvis-1); b(1,:)=0; b(Nhid,:)=0; b(:,Nvis)=0; b(1,Nvis)=1; b(Nhid,Nvis)=1; % %treinando com a sequencia % delta_max=inf; delta_thresh=1e-3; numiter=0; while delta_max>delta_thresh a0=a; b0=b; for s=1:Nseq %calcula alpha,beta, gamma e xi [alpha,beta,gamma,xi]=fwd_bkwd(a,b,V{s}); Gamma{s}=gamma; Xi{s}=xi; end % atualiza matrizes a e b [a,b]=update(a,b,Gamma,Xi,V); %verificao de convergncia delta_a=max(max(abs(a-a0))); delta_b=max(max(abs(b-b0))); delta_max=max(delta_a,delta_b); numiter=numiter+1; end fprintf('treinado com %d interacoes ',numiter) %% function[Pv]=evaluate(V,a,b) %Pv=evaluate(V,a,b) % T=length(V)-1; Nhid=size(a,1); alpha=fwd_alg(a,b,V); Pv=sum(alpha(:,T)) %% %% %carregar dados [V1,V2]=load_data_hmm(); % Nhid=5; Nvis=5; [a1,b1]=train(V1,Nhid,Nvis); [a2,b2]=train(V2,Nhid,Nvis);

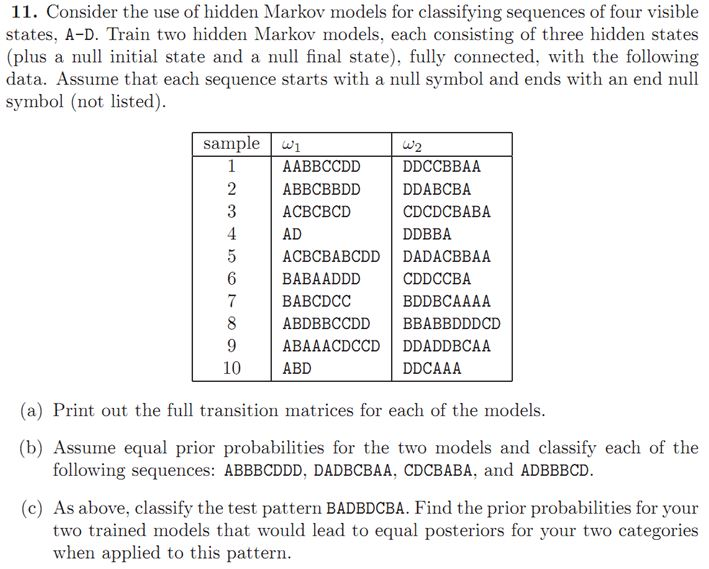
11. Consider the use of hidden Markov models for classifying sequences of four visible states, A-D. Train two hidden Markov models, each consisting of three hidden states (plus a null initial state and a null final state), fully connected, with the following data. Assume that each sequence starts with a null symbol and ends with an end null symbol (not listed). sample wi AA BBCCDD DDCCBBA A. BBCBBDD DDABCBA. ACBCBCD CDCDCBABA. AD DDBBA ACBC BABCDD DADA CBBAA BABA ADDD CDDCCBA 7 BABCDCC BDDBCAAAA 8 ABD BBCCDD BBA BBDDDCD 9 ABAA ACDCCD DDADDBCAA 10 ABD DDCAAA a) Print out the full transition matrices for each of the models (b) Assume equal prior probabilities for the two models and classify each of the following sequences: ABBBCDDD, DADBCBAA, CDCBABA, and ADBBBCD. (c) As above, classify the test pattern BADBDCBA. Find the prior probabilities for your two trained models that would lead to equal posteriors for your two categories when applied to this pattern. 11. Consider the use of hidden Markov models for classifying sequences of four visible states, A-D. Train two hidden Markov models, each consisting of three hidden states (plus a null initial state and a null final state), fully connected, with the following data. Assume that each sequence starts with a null symbol and ends with an end null symbol (not listed). sample wi AA BBCCDD DDCCBBA A. BBCBBDD DDABCBA. ACBCBCD CDCDCBABA. AD DDBBA ACBC BABCDD DADA CBBAA BABA ADDD CDDCCBA 7 BABCDCC BDDBCAAAA 8 ABD BBCCDD BBA BBDDDCD 9 ABAA ACDCCD DDADDBCAA 10 ABD DDCAAA a) Print out the full transition matrices for each of the models (b) Assume equal prior probabilities for the two models and classify each of the following sequences: ABBBCDDD, DADBCBAA, CDCBABA, and ADBBBCD. (c) As above, classify the test pattern BADBDCBA. Find the prior probabilities for your two trained models that would lead to equal posteriors for your two categories when applied to this pattern