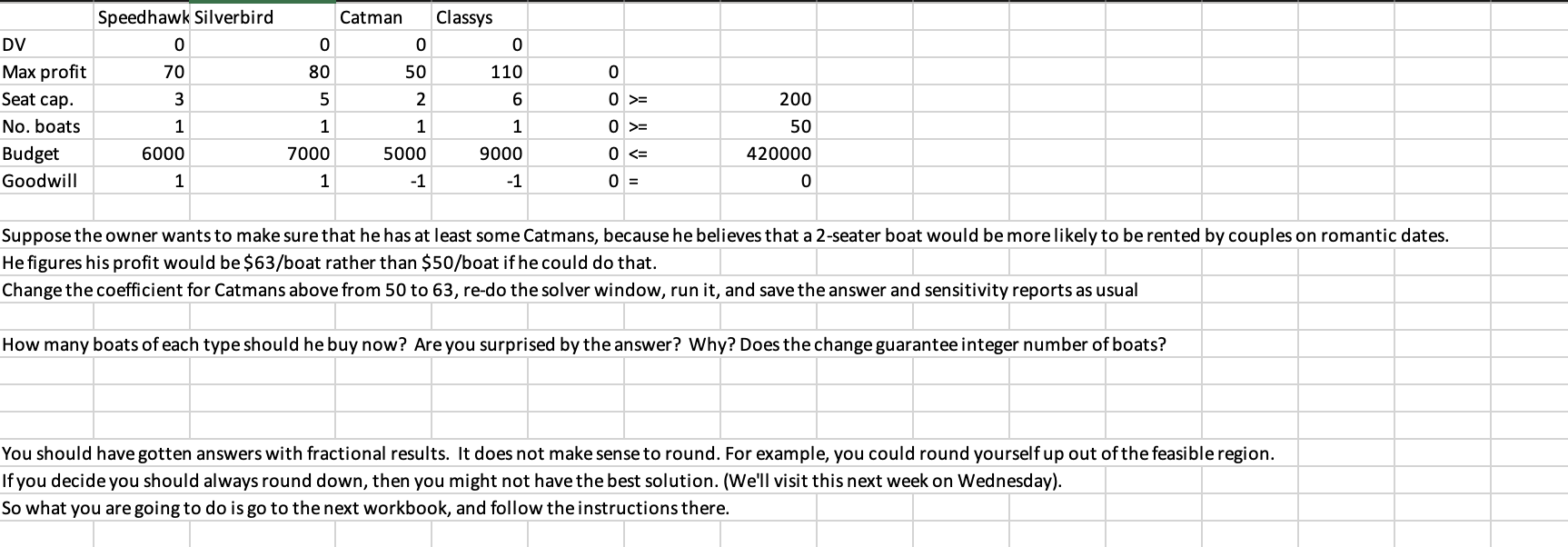
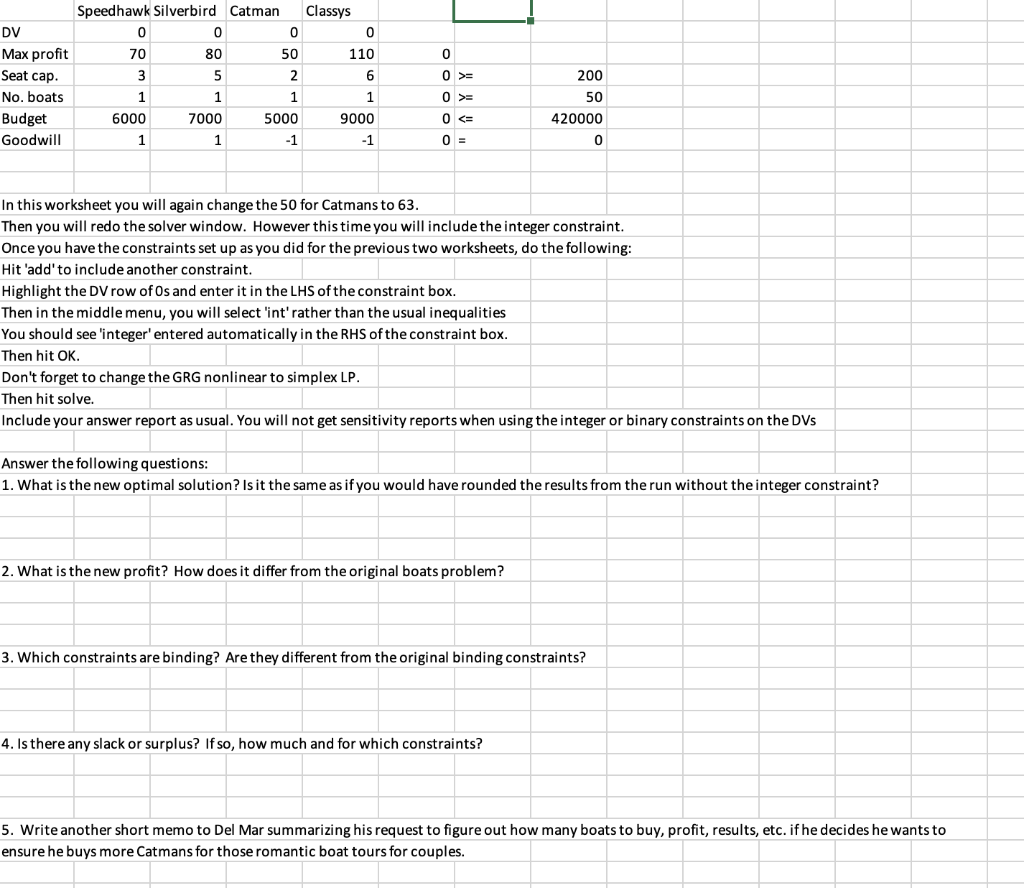
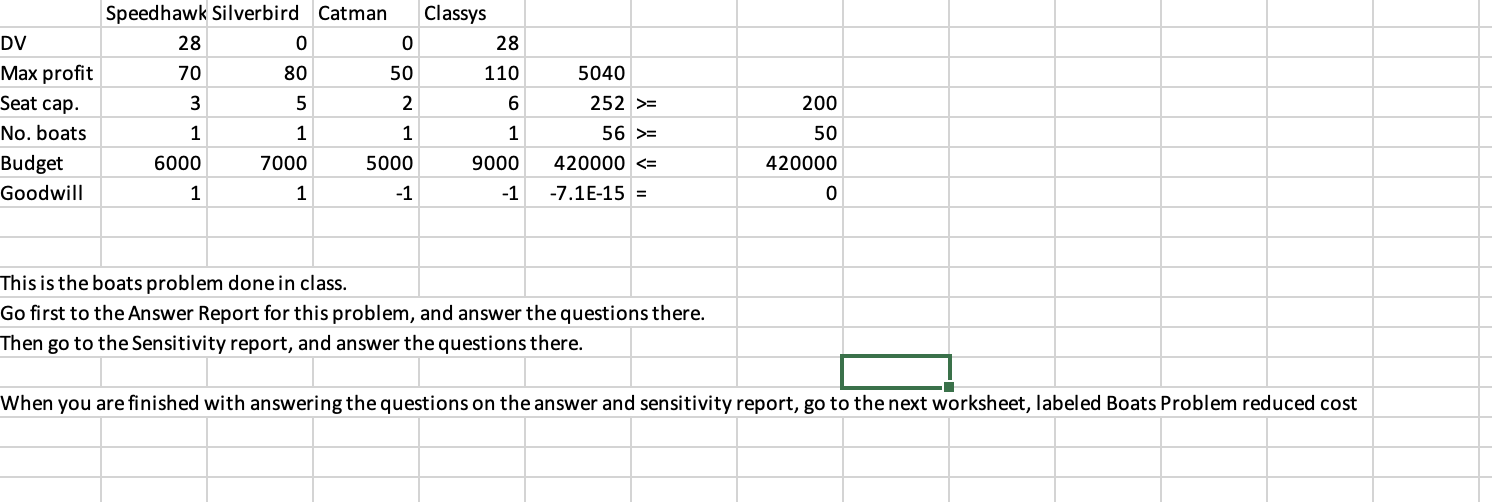
Constraints Questions on the top sensitivity report. 1. When are the values of reduced cost 0 ? 2. When are the values of reduced cost non-zero? 3. Reduced cost is the amount you have to change a DVs objective function coefficient by in order to get the DV to be non-zero. What is the relationship you see between reduced cost and allowable increase or decrease? The fact that reduced cost is determined terms of cost rather than profit explains the negative sign. Our objective function is profit. You should go by the allowable increase/decrease that the reduced cost refers to. Questions on the bottom sensitivity report. 1. Which constraints have 0 Shadow Price? Which have non-zero shadow price? 2. If you increased the minimum number of seats from 200 to 250, would the Shadow Price change? Explain your reasoning or no credit. 3. What is the change in profit if the minimum number of boats is increased from 200 to 250 ? (Use the shadow price formulat given in class: SP= (change in objective function value / (change in RHS of constraint) 4. Suppose the minimum number of boats required is still 200, but an emergency has come up, so the owner has to dive into his budget to take care of that emergency. The amount available for boats is now $400,000 rather than $420,000. Would the optimal solution change? Explain your reasoning or no credit. 5. What is the change in profit if the budgeted amount is decreased to $400,000 from $420,000. Use the SP formula as above. 6. Suppose despite the drop in budgeted amount, the owner would still like to try to increase the number of seats, but to a more modest 25 additional seats. Use the 100% rule to see if the shadow prices for both constraints stay the same with these two changes. 7. Given your answer in 6 above, if possible, calculate the change in total profit from the two changes (budget now $400,000 and minimum number of seats desired now 225) using the individual show prices for each constraint, and summing the results If it is not possible to calculate the change in profit, explain why not. Suppose the owner wants to make sure that he has at least some Catmans, because he believes that a 2 -seater boat would be more likely to be rented by couples on romantic dates. He figures his profit would be $63/ boat rather than $50/ boat if he could do that. Change the coefficient for Catmans above from 50 to 63 , re-do the solver window, run it, and save the answer and sensitivity reports as usual How many boats of each type should he buy now? Are you surprised by the answer? Why? Does the change guarantee integer number of boats? You should have gotten answers with fractional results. It does not make sense to round. For example, you could round yourself up out of the feasible region. If you decide you should always round down, then you might not have the best solution. (We'll visit this next week on Wednesday). So what you are going to do is go to the next workbook, and follow the instructions there. \begin{tabular}{|l|r|r|r|r|r|r|r|} & Speedhawk Silverbird & Catman & \multicolumn{2}{l|}{ Classys } & \\ \hline DV & 0 & 0 & 0 & 0 & & \\ \hline Max profit & 70 & 80 & 50 & 110 & 0 & \\ \hline Seat cap. & 3 & 5 & 2 & 6 & 0>= & 200 \\ \hline No. boats & 1 & 1 & 1 & 1 & 0>= & 50 \\ \hline Budget & 6000 & 7000 & 5000 & 9000 & 0= & 50 \\ \hline No. boats & 1 & 1 & 1 & 1 & 56>= & 420000 \\ \hline Budget & 6000 & 7000 & 5000 & 9000 & 420000= & 200 \\ \hline No. boats & 1 & 1 & 1 & 1 & 0>= & 50 \\ \hline Budget & 6000 & 7000 & 5000 & 9000 & 0= & 50 \\ \hline No. boats & 1 & 1 & 1 & 1 & 56>= & 420000 \\ \hline Budget & 6000 & 7000 & 5000 & 9000 & 420000