_{Constructing Confidence Intervals}

• In the discussion for week 4, you rolled a pair of dice 10 times and calculated the average sum of your rolls.Then you did the same thing with 20 rolls.
• Use your results from the week 4 discussion for the average of 10 rolls and for the average of 20 rolls to construct a confidence interval for the true mean of the sum of a pair of dice (assume ? = 2.41).
• What do you notice about the length of the interval for the mean of 10 rolls versus the mean of 20 rolls?Did you expect this?Why or why not?

Week 4 Discussion

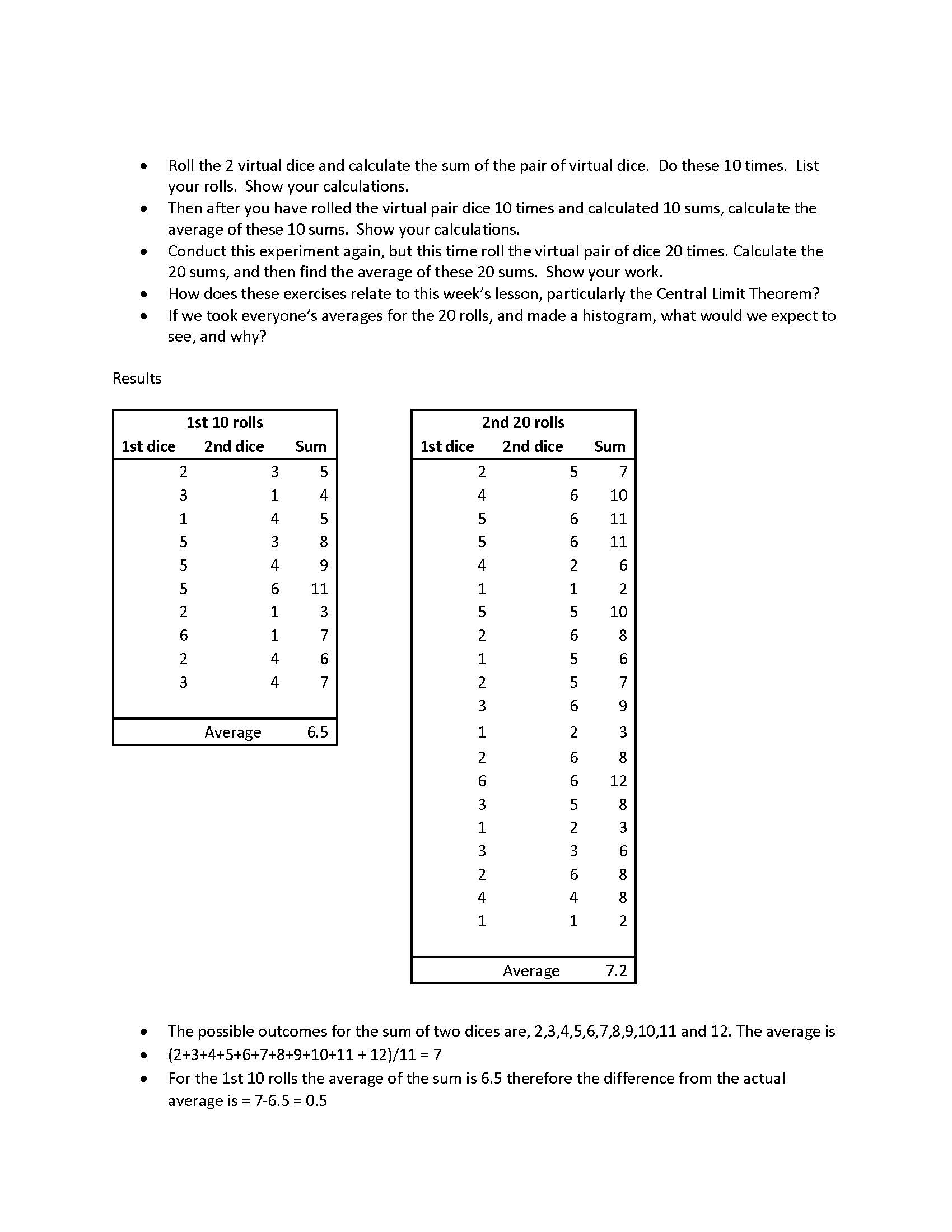
Results Roll the 2 virtual dice and calculate the sum of the pair of virtual dice. Do these 10 times. List your rolls. Show your calculations. Then after you have rolled the virtual pair dice 10 times and calculated 10 sums, calculate the average of these 10 sums. Show your calculations. Conduct this experiment again, but this time roll the virtual pair of dice 20 times. Calculate the 20 sums, and then find the average of these 20 sums. Show your work. How does these exercises relate to this week's lesson, particularly the Central Limit Theorem? If we took everyone's averages for the 20 rolls, and made a histogram, what would we expect to see, and why? lst 10 rolls 2nd 20 rolls lst dice 2nd dice Sum lst dice 2nd dice Sum wNmNmmmi'ww ##i'l'O-lhw-lhi'w Average HgmmmmmmNmmmmmi'Mmmmm 2 4 5 5 4 1 5 2 1 2 3 1 2 6 3 1 3 2 4 1 Average The possible outcomes for the sum of two dices are, 2,3,4,5,6,7,8,9,10,11 and 12. The average is (2+3+4+5+6+7+8+9+10+11 + 12)/11 = 7 For the lst 10 rolls the average of the sum is 6.5 therefore the difference from the actual average is = 76.5 = 0.5