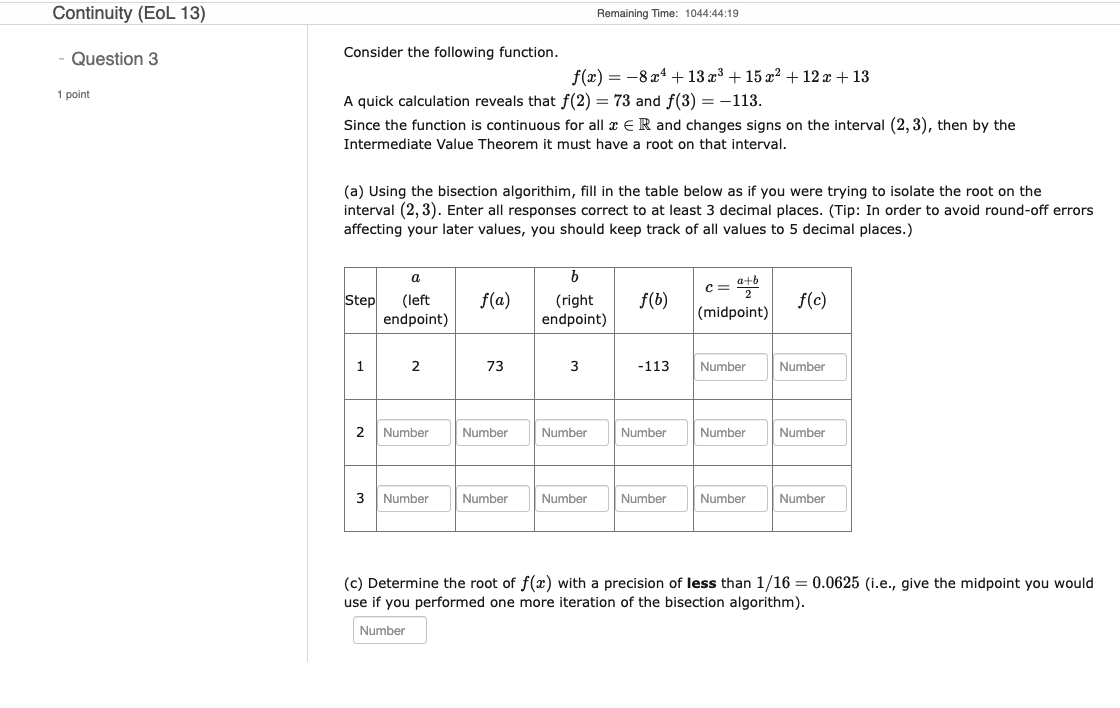
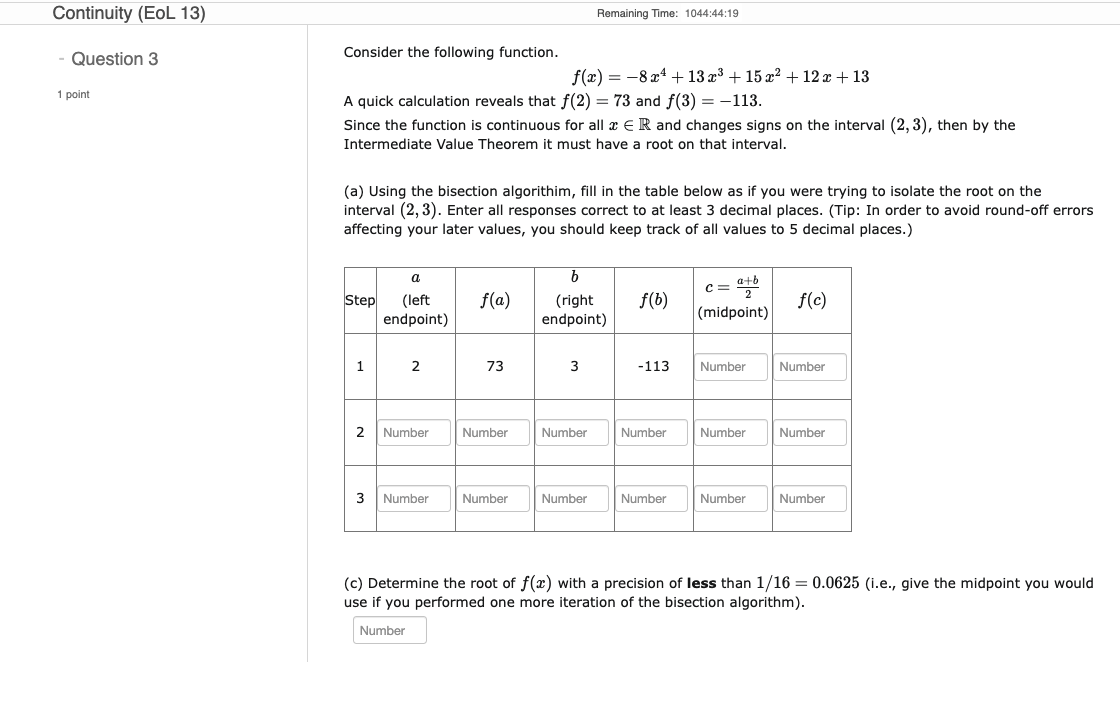
Continuity (EOL 13) Remaining Time: 1044:44:19 Question 3 Consider the following function. f(x) = -824+13x3 + 1523 +12x + 13 1 point A quick calculation reveals that f(2) = 73 and f(3) = -113. Since the function is continuous for all i E IR and changes signs on the interval (2, 3), then by the Intermediate Value Theorem it must have a root on that interval. (a) Using the bisection algorithm, fill in the table below as if you were trying to isolate the root on the interval (2, 3). Enter all responses correct to at least 3 decimal places. (Tip: In order to avoid round-off errors affecting your later values, you should keep track of all values to 5 decimal places.) a b C - atb Step (left f(a) (right f(b) f(c) endpoint) endpoint) (midpoint) 1 2 73 -113 Number Number 2 Number Number Number Number Number Number 3 Number Number Number Number Number Number (c) Determine the root of f() with a precision of less than 1/16 = 0.0625 (i.e., give the midpoint you would use if you performed one more iteration of the bisection algorithm). Number