convert the following C code to x86 assembly

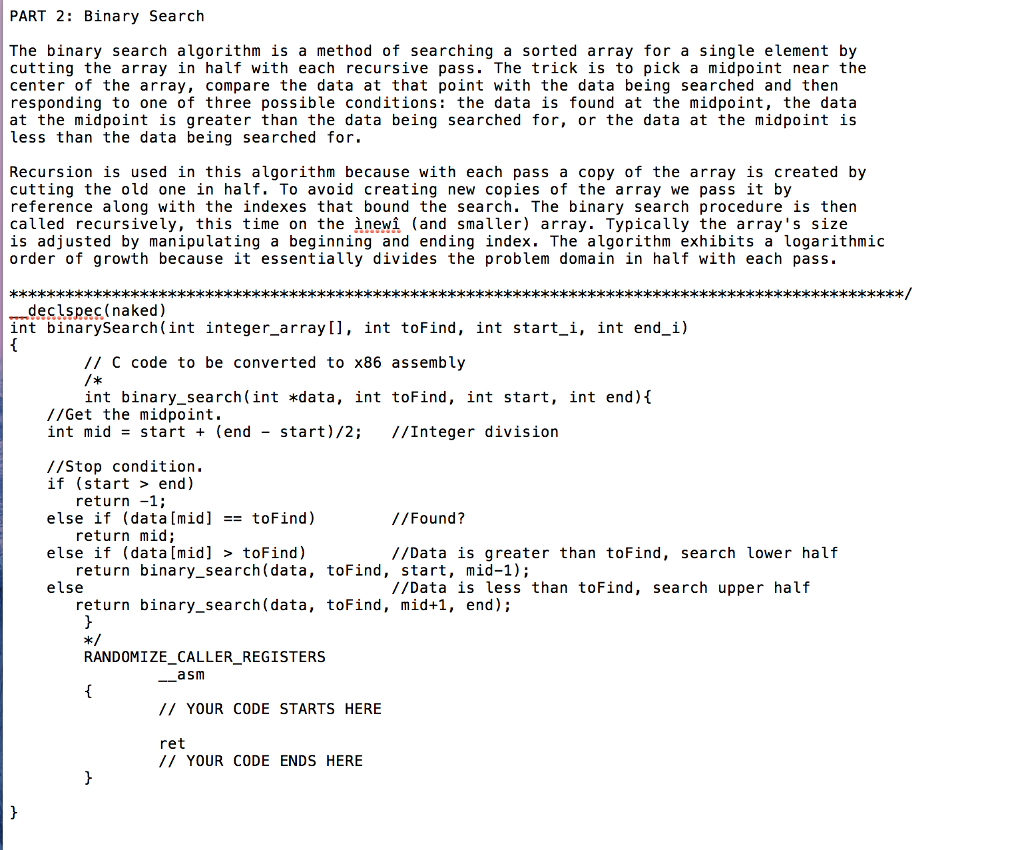
PART 2: Binary Search The binary search algorithm is a method of searching a sorted array for a single element by cutting the array in half with each recursive pass. The trick is to pick a midpoint near the center of the array, compare the data at that point with the data being searched and then responding to one of three possible conditions: the data is found at the midpoint, the data at the midpoint is greater than the data being searched for, or the data at the midpoint is Less than the data being searched for. Recursion is used in this algorithm because with each pass a copy of the array is created by cutting the old one in half. To avoid creating new copies of the array we pass it by reference along with the indexes that bound the search. The binary search procedure is then called recursively, this time on the inewi (and smaller) array. Typically the array's size is adjusted by manipulating a beginning and ending index. The algorithm exhibits a logarithmic order of growth because it essentially divides the problem domain in half with each pass. declspec( naked ) int binarySearch (int integer_array], int toFind, int start_i, int end_i) // C code to be converted to x86 assembly int binary_search(int *data, int toFind, int start, int end) //Get the midpoint. int mid = start + (end - start ) /2; //Integer division //Stop condition. if (start > end) else if (data [mid] = toFind) else if (data[mid] > toFind) else return -1; return mid; return binary_search (data, toFind, start, mid-1); return binary_search(data, toFind, mid+1, end); //Found? //Data is greater than toFind, search lower half //Data is less than toFind, search upper half RANDOMIZE CALLER REGISTERS asm // YOUR CODE STARTS HERE ret // YOUR CODE ENDS HERE PART 2: Binary Search The binary search algorithm is a method of searching a sorted array for a single element by cutting the array in half with each recursive pass. The trick is to pick a midpoint near the center of the array, compare the data at that point with the data being searched and then responding to one of three possible conditions: the data is found at the midpoint, the data at the midpoint is greater than the data being searched for, or the data at the midpoint is Less than the data being searched for. Recursion is used in this algorithm because with each pass a copy of the array is created by cutting the old one in half. To avoid creating new copies of the array we pass it by reference along with the indexes that bound the search. The binary search procedure is then called recursively, this time on the inewi (and smaller) array. Typically the array's size is adjusted by manipulating a beginning and ending index. The algorithm exhibits a logarithmic order of growth because it essentially divides the problem domain in half with each pass. declspec( naked ) int binarySearch (int integer_array], int toFind, int start_i, int end_i) // C code to be converted to x86 assembly int binary_search(int *data, int toFind, int start, int end) //Get the midpoint. int mid = start + (end - start ) /2; //Integer division //Stop condition. if (start > end) else if (data [mid] = toFind) else if (data[mid] > toFind) else return -1; return mid; return binary_search (data, toFind, start, mid-1); return binary_search(data, toFind, mid+1, end); //Found? //Data is greater than toFind, search lower half //Data is less than toFind, search upper half RANDOMIZE CALLER REGISTERS asm // YOUR CODE STARTS HERE ret // YOUR CODE ENDS HERE