*& correct answers only

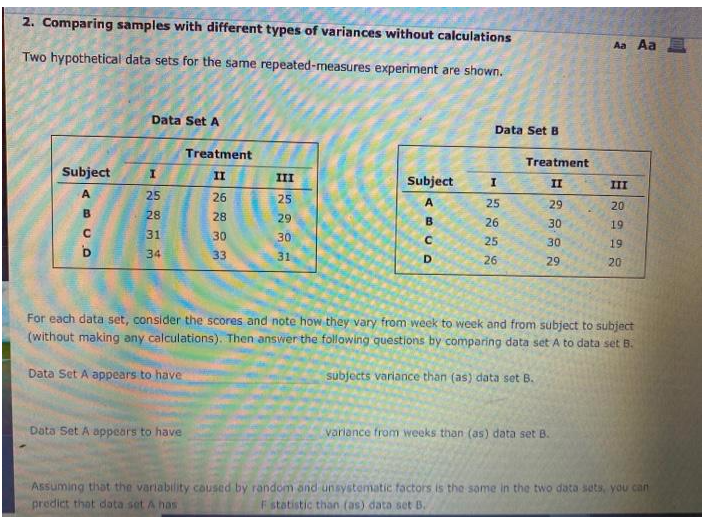
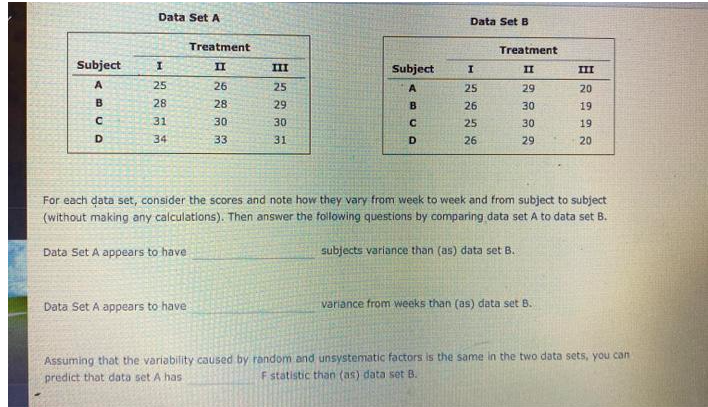
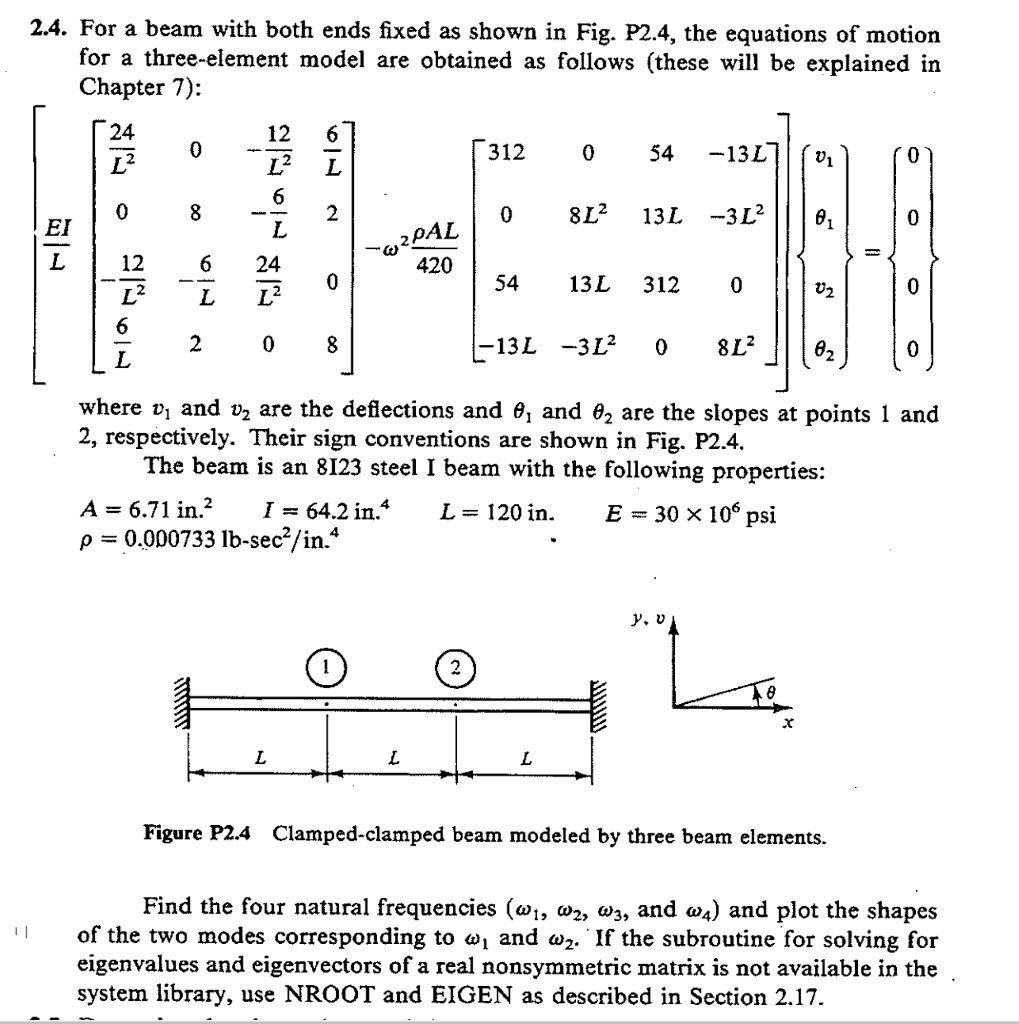
1. Solve the initial-value problem using Modified Euler method 2-20 ost s1,y(0) - 1, withh - 0.1 2. Solve the System of first order differential equations as shown below by applying Runge-Kutta fourth order method and Compare the results with the actual solutions 1(1 )=-121 +12 +21- du dr =1 -1, +2, 0sis1, u (0)=-1, h=0.1 dt = -11, +My +41, Ostsl, u, (0)=0, h=0.1 3. Use Newton's method to find a solution with at least 6 significant digits near x=2 and y=3 of the system consisting of both of the following equations: f(xy)= + sin(3xy)+ x In(y)-70=0 and g(x, y) - x cos (2y)+ xe -+ xIn (x)-70-0. 4. Find the value of vi+ x using Simpson's 3/8 th rule.2.4-2.9 Find the Euler-Lagrange equations and the natural boundary conditions associated with each of the total potential energy functionals given in Problems 2.4 2.9. The dependent variables are listed as the arguments of the functional, and only the geometric boundary conditions are stated. No other variables are functions of the dependent variables, but may be functions of position in the domain or on the boundary. 2.4 Arial deformation of a spring-supported bar: ".(0) = 0 II(uo) = EA dra - fun di + "[uo( [)]? - Pro(I) 2.5 Bending of a beam on clastic foundation: w(0) = w(b) =0 I(wo) = EI up - qua de 2.6 Nonlinear bending of a beam: 10(0) = 0. up(0) =0, and (dab/de)(0) = 0 - Fold ( L) - Puo( L) 2.7 Transverse deflection of a membrane: * = 0 on the portion I's of the total boundary I (Ta = [- Ie) II(u) = du 2 + 022 dy - fu drdy - tu da 2.8 Bending of an orthotropic plate: un =0, Own/On =0 on the boundary I 2 + 2Den 8-wo droy 2 + - quo dady1. Bending a beam (1D version): An elastic beam is supported at its ends and loaded by a distributed load, p(x). The elastic strain energy stored in a bent beam and the loading energy are given by: Total [u(x)] - Isending [u(2)] + Illandtu( z)] (1) (2) Iload [u(x)] - - p(x)u(x) dr. (3) (a) Suppose the beam is simply supported. i. Write down the class of admissible solutions and admissible variations to minimize IItotal [u( x)]. ii. Derive the Euler-Lagrange equations that stem from minimizing Itstar. Clearly identify the boundary conditions. How many essential boundary conditions? How many natural boundary conditions? ili. Consider the special case of a point load in the center of the beam, for which: p(x) = Pi(x - L/2) (4) Here, 6(r) is the Dirac delta function. Confirm that Iload simplies to become: Ijoadfu(x)] = -Pu(L/2). (5) iv. Choose a suitable trial solution o(x), and let u(x) ~ do(x), where d is an undetermined constant. For Had given in equation (5), minimize It{do(x)] with respect to d, to estimate u(L/2) ~ do( L/2) (6) Compare to the known exact solution. (b) Select two different functions (r) and oz(r). Let u(x) =dad.(1) (7) n=1 Evaluate dn, n = 1, 2 for your choice of on(r). Feel free to evaluate your integrals numerically via computer; try to accomplish your goal with as little human effort as possible. How hard would it be to consider larger number of NV functions, on(I)?1. (11 marks) It can be shown that a vibrations in a uniform elastic beam of length L satisfy the fourth-order PDE at2 ax4 where u represents the displacement of the bar, x represents the distance along the bar, t represents time. Suppose that the ends of the bar are both kept stationary with zero displacement. (a) How many boundary and initial conditions are required to solve the PDE ? Write down the boundary conditions. (b) Use separation of variables to show that the X-equation can be written as X"" - B*X =0 and hence find the solutions: X(x) = A cos( Bx) + B sin(Bx) + C cosh(Bx) + D sinh(Bx) T(t) = a cos(cB't) + bsin(cB2t) for constants A, B, C, D, a, b and B. (c) Use the boundary conditions at x = 0 to eliminate C and D from the above expression for X(x). (d) Show that for non trivial solutions we require that Y cos( BL) cosh (L) = 1 in (Solving the above equation numerically for B gives you the to "natural modes of vibration" for the bar. Our old friend Steven of Strogatz can tell you that these have great significance when it comes to building bridges!)2.4. For a beam with both ends xed as shown in Fig. P14, the equations of motion for a three-element model are obtained as follows (these will be explained in Chaplet-7): % {3 a; % 312 o 54 -13L v1 0 E! o s E 2 \"43% 0 8L" 13L ~31} 9; a 0 L \"% \"E g 0 42 54 13L 312 o v; 0 E 2 o s -13L 3L'1 0 3L2 62 0 where 131 and 122 are the deections and 31 and 62 are the slopes at points 1 and 2, respectively. Their sign conVentions are shown in Fig. P2.4. The beam is an 8123 steel I beam with the following properties: A = 6.71 in.2 I = 64.2111} L =120in. E -= 30 x 10' psi p =_D.,000733 lb-see2 in.4 " J'. I? .. (D G) I 18 x I L l I. I L I Figure P24 damped-clamped beam modeled by three beam elements. Find the four natural frequencies (ml, mg, :3, and (:34) and plot the shapes of the two modes corresponding to all and m2.'1f the subroutine 'for solving for eigenvalues and eigenvectors of a real nonsymmetiic matrix is not available in the _ system library, use NROOT and EIGEN as described in Section 2.17