Could I please have the worked solution to the following question:

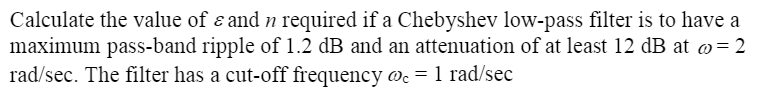
A Chebyshev filter is described by a squared-magnitude function: G(j)2=1+2[Cn(c)]21 where is the ripple factor and c is the cut-off frequency of the filter. The nth order Chebyshev polynomial, Cn(c), for c1 is defined as: Cn(c)=cos(ncos1(c)) Prove that in the stop-band of the filter the attenuation, at a given frequency , is approximately given by: X(indB)20log10+6(n1)+20nlog10(c) Make the assumption that for large values of (in the stop-band of the filter) the following approximation of an nth order Chebyshev polynomial is valid: Cn(c)2n1(c)n Calculate the value of and n required if a Chebyshev low-pass filter is to have a maximum pass-band ripple of 1.2dB and an attenuation of at least 12dB at =2 rad/sec. The filter has a cut-off frequency c=1rad/sec Determine the analogue transfer function, G(s), of a second order, i.e. n=2, Chebyshev low-pass filter. Note: Use should be made of the following relations between the Butterworth and Chebyshev pole locations for an nth order filter: Re[ Chebyshev 1]=Re[ Butterworth n]xtanhA Im[ Chebyshev 1]=Re[ Butterworth n] Chebyshev2 = Chebyshev1 xcoshA (where: A=n1sinh1(1) ) and also the fact that for a Butterworth filter of order n, the angle of the kth pole, k, to the real axis of the s-domain is given by: k=nknodd or k=n(k+21)neven