Could somebody help me finish up the following python problem. I am not sure how to evaluate the least squares fit. I will post the problem and what code I have as both screenshots and text to avoid any formatting issues on this website. You do not need to worry about plotting or anything I can handle all of the nitty gritty work I just am not sure how to write the functions.

Also here is the text file if you would like to test/see.

-4.0, 0.8563140883827762 -3.9396984924623117, 0.9167031468310413 -3.879396984924623, 0.9623951734770443 -3.819095477386935, 0.9954310088580303 -3.758793969849246, 1.0222562263709822 -3.698492462311558, 1.0515834532419164 -3.6381909547738696, 1.0922895735642177 -3.577889447236181, 1.15205934856525 -3.5175879396984926, 1.2366997128074049 -3.457286432160804, 1.3496729647128458 -3.3969849246231156, 1.4914909848399456 -3.3366834170854274, 1.6589631900696922 -3.2763819095477387, 1.8446762078882428 -3.2160804020100504, 2.0372942514231918 -3.1557788944723617, 2.223111656305757 -3.0954773869346734, 2.3887290935274 -3.035175879396985, 2.5240451191558124 -2.9748743718592965, 2.6244383827496565 -2.914572864321608, 2.691343790213912 -2.8542713567839195, 2.7311879303463282 -2.7939698492462313, 2.7533235960222697 -2.733668341708543, 2.7678153661180036 -2.6733668341708543, 2.7836971575237155 -2.6130653266331656, 2.8079243484523904 -2.5527638190954773, 2.8449339767525785 -2.492462311557789, 2.896601215423138 -2.432160804020101, 2.962400600141147 -2.371859296482412, 3.039664535013458 -2.3115577889447234, 3.123913972388667 -2.251256281407035, 3.2092832972683265 -2.190954773869347, 3.289065150968866 -2.1306532663316586, 3.3563693135757897 -2.07035175879397, 3.4048412625944517 -2.0100502512562812, 3.4293438291809872 -1.949748743718593, 3.4264897769240923 -1.8894472361809047, 3.3949333734738047 -1.829145728643216, 3.3353791527262424 -1.7688442211055277, 3.250327929079009 -1.7085427135678395, 3.1436322565700654 -1.6482412060301508, 3.0199607321346664 -1.5879396984924625, 2.88426909256649 -1.5276381909547738, 2.7413526547918243 -1.4673366834170856, 2.595521220251848 -1.4070351758793973, 2.4504054670314472 -1.3467336683417086, 2.3088802814643716 -1.2864321608040203, 2.173077722918645 -1.2261306532663316, 2.044459014712137 -1.1658291457286434, 1.9239180261769249 -1.1055276381909547, 1.8118949340242434 -1.0452261306532664, 1.7084856495396816 -0.9849246231155782, 1.613538686917582 -0.9246231155778895, 1.5267357930125152 -0.8643216080402012, 1.4476557936107168 -0.8040201005025125, 1.3758229661426264 -0.7437185929648242, 1.3107421545771951 -0.683417085427136, 1.251923117798056 -0.6231155778894473, 1.198896504656018 -0.562814070351759, 1.1512235607449637 -0.5025125628140703, 1.108501312994641 -0.44221105527638205, 1.0703646185645337 -0.3819095477386938, 1.0364861405779717 -0.3216080402010051, 1.0065750398466027 -0.2613065326633168, 0.9803749513265934 -0.20100502512562812, 0.9576616425179393 -0.14070351758793986, 0.9382406213970336 -0.0804020100502516, 0.9219448660084467 -0.0201005025125629, 0.9086327790825945 0.0402010050251258, 0.8981864223157419 0.10050251256281406, 0.8905100504826332 0.16080402010050232, 0.8855289404505441 0.22110552763819058, 0.883188490263297 0.28140703517587884, 0.8834535451783065 0.341708542713568, 0.8863078877027081 0.40201005025125625, 0.8917538044061659 0.4623115577889445, 0.8998116109020211 0.5226130653266328, 0.9105189753644447 0.582914572864321, 0.9239298280031546 0.6432160804020102, 0.9401125772287591 0.7035175879396984, 0.9591472719269734 0.7638190954773867, 0.9811212542193531 0.824120603015075, 1.0061227424060926 0.8844221105527632, 1.0342316788850747 0.9447236180904524, 1.0655070905662347 1.0050251256281406, 1.0999701699559548 1.0653266331658289, 1.1375823410387544 1.1256281407035171, 1.1782177937451643 1.1859296482412054, 1.2216304444601171 1.2462311557788945, 1.2674161131246753 1.3065326633165828, 1.314971999723948 1.366834170854271, 1.3634573457273609 1.4271356783919593, 1.4117614127023688 1.4874371859296476, 1.4584873230951554 1.5477386934673367, 1.501962305207634 1.608040201005025, 1.540285540266711 1.6683417085427132, 1.5714229527951733 1.7286432160804015, 1.5933528219578679 1.7889447236180906, 1.6042565809507816 1.849246231155779, 1.6027365341589364 1.9095477386934672, 1.5880292322039906 1.9698492462311554, 1.5601743171682478 2.0301507537688437, 1.5200985417112634 2.090452261306533, 1.4695862624320553 2.150753768844221, 1.4111298411182125 2.2110552763819094, 1.3476801243051744 2.2713567839195976, 1.2823395818427963 2.331658291457286, 1.2180506682858065 2.391959798994975, 1.1573261827103336 2.4522613065326633, 1.1020499649734272 2.5125628140703515, 1.0533532690846974 2.57286432160804, 1.0115540201699187 2.633165829145728, 0.976140063990701 2.693467336683417, 0.9457863333322579 2.7537688442211055, 0.9184173570694325 2.8140703517587937, 0.8913524667581647 2.874371859296482, 0.8615858790534634 2.9346733668341702, 0.8262364797760368 2.9949748743718594, 0.783136797364218 3.0552763819095476, 0.7314280982140479 3.115577889447236, 0.6719429660304204 3.175879396984924, 0.6071677746328559 3.2361809045226124, 0.5407251864820007 3.2964824120603016, 0.47653830310202666 3.35678391959799, 0.41798954119725706 3.417085427135678, 0.36736134635464013 3.4773869346733663, 0.3256703635504213 3.5376884422110546, 0.2928138816353891 3.5979899497487438, 0.26785261684563105 3.658291457286432, 0.24927830967838566 3.7185929648241203, 0.2352074361957352 3.7788944723618085, 0.22354105332785587 3.839195979899497, 0.2121869120392534 3.899497487437186, 0.19941271110395198 3.959798994974874, 0.18427336599824223 4.0201005025125625, 0.16690110331475802 4.080402010050252, 0.14842712841106118 4.140703517587939, 0.13050952894595477 4.201005025125628, 0.11471855099265298 4.2613065326633155, 0.10210279262707515 4.321608040201005, 0.09307166493044448 4.381909547738694, 0.08749531505251872 4.442211055276381, 0.084841898939101 4.50251256281407, 0.08424880425132493 4.562814070351758, 0.0845616041078291 4.623115577889447, 0.08447779806880622 4.683417085427136, 0.0829032405708677 4.743718592964823, 0.07941397967378727 4.8040201005025125, 0.07448996148834346 4.8643216080402, 0.06928587420593556 4.924623115577889, 0.06510799155512474 4.984924623115578, 0.06298364089721811 5.0452261306532655, 0.06350019323327172 5.105527638190955, 0.06678055186772616 5.165829145728642, 0.07239616897897332 5.226130653266331, 0.07922175127905644 5.28643216080402, 0.08553875709770253 5.346733668341708, 0.08972828236299726 5.407035175879397, 0.09131127542589176 5.467336683417084, 0.0914491109744875 5.527638190954773, 0.09243692053501908 5.5879396984924625, 0.09677978479731741 5.64824120603015, 0.10655732680221183 5.708542713567839, 0.12296880392288867 5.768844221105526, 0.14553697338125846 5.829145728643216, 0.17119027210994878 5.889447236180905, 0.19482941256003325 5.949748743718592, 0.21261348314748912 6.010050251256281, 0.2257041679894202 6.070351758793969, 0.24063394645871097 6.130653266331658, 0.26654029941773644 6.190954773869347, 0.3122787854465921 6.251256281407034, 0.38352619539657984 6.311557788944723, 0.47772497655139856 6.371859296482411, 0.5795382289049789 6.4321608040201, 0.6672118448458824 6.492462311557789, 0.7321369239947321 6.5527638190954764, 0.7918273949273762 6.613065326633166, 0.8822150320930118 6.673366834170853, 1.0416388009283872 6.733668341708542, 1.2949880042168174 6.793969849246231, 1.6293512215731212 6.854271356783919, 1.9737933584710665 6.914572864321608, 2.2368303492240362 6.974874371859295, 2.400392466198928 7.035175879396984, 2.556167925821477 7.0954773869346734, 2.8429158170410105 7.155778894472361, 3.3683371298932494 7.21608040201005, 4.135657524682739 7.276381909547737, 4.963528101503408 7.3366834170854265, 5.545261876005398 7.396984924623116, 5.748119639162751 7.457286432160803, 5.793561998324683 7.517587939698492, 6.050722993477291 7.577889447236181, 6.759732778484411 7.638190954773869, 7.863757688480311 7.698492462311558, 8.902951592925117 7.758793969849245, 9.272377379196506 7.819095477386934, 8.895522112711287 7.8793969849246235, 8.350609026599752 7.939698492462311, 8.23836362978743 8.0, 8.729958936798685

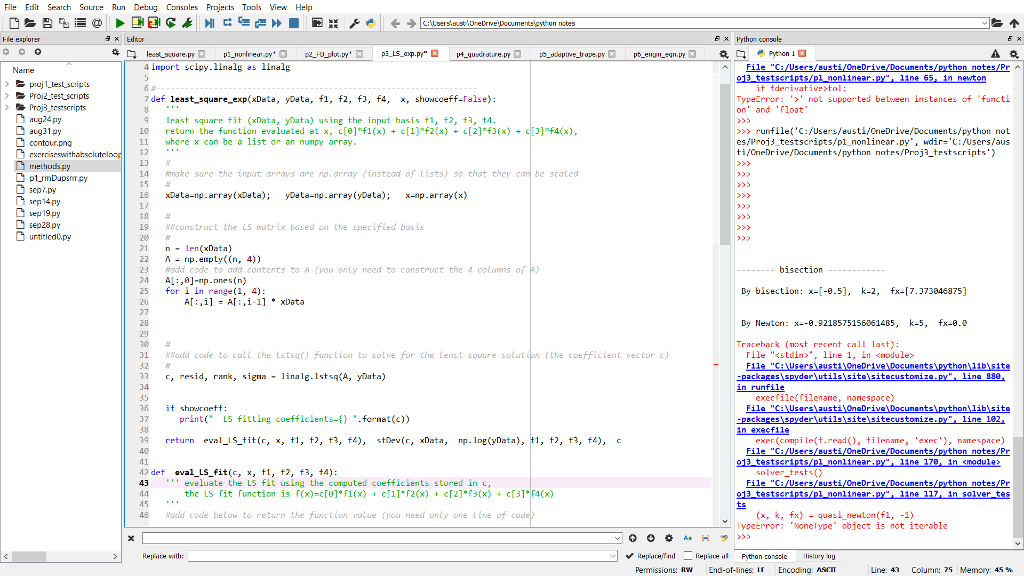
Current code but formatting will get ruined by chegg. :(

def least_square_exp(xData, yData, f1, f2, f3, f4, x, showcoeff=False): ''' least square fit (xData, yData) using the input basis f1, f2, f3, f4. return the function evaluated at x, c[0]*f1(x) + c[1]*f2(x) + c[2]*f3(x) + c[3]*f4(x), where x can be a list or an numpy array. ''' # #make sure the input arrays are np.array (instead of lists) so that they can be scaled # xData=np.array(xData); yData=np.array(yData); x=np.array(x)

# ##construct the LS matrix based on the specified basis # n = len(xData) A = np.empty((n, 4)) #add code to add contents to A (you only need to construct the 4 columns of A) A[:,0]=np.ones(n) for i in range(1, 4): A[:,i] = A[:,i-1] * xData

# ##add code to call the lstsq() function to solve for the least square solution (the coefficient vector c) # c, resid, rank, sigma = linalg.lstsq(A, yData)

if showcoeff: print(" LS fitting coefficients={} ".format(c))

return eval_LS_fit(c, x, f1, f2, f3, f4), stDev(c, xData, np.log(yData), f1, f2, f3, f4), c

def eval_LS_fit(c, x, f1, f2, f3, f4): ''' evaluate the LS fit using the computed coefficients stored in c, the LS fit function is f(x)=c[0]*f1(x) + c[1]*f2(x) + c[2]*f3(x) + c[3]*f4(x) ''' #add code below to return the function value (you need only one line of code)

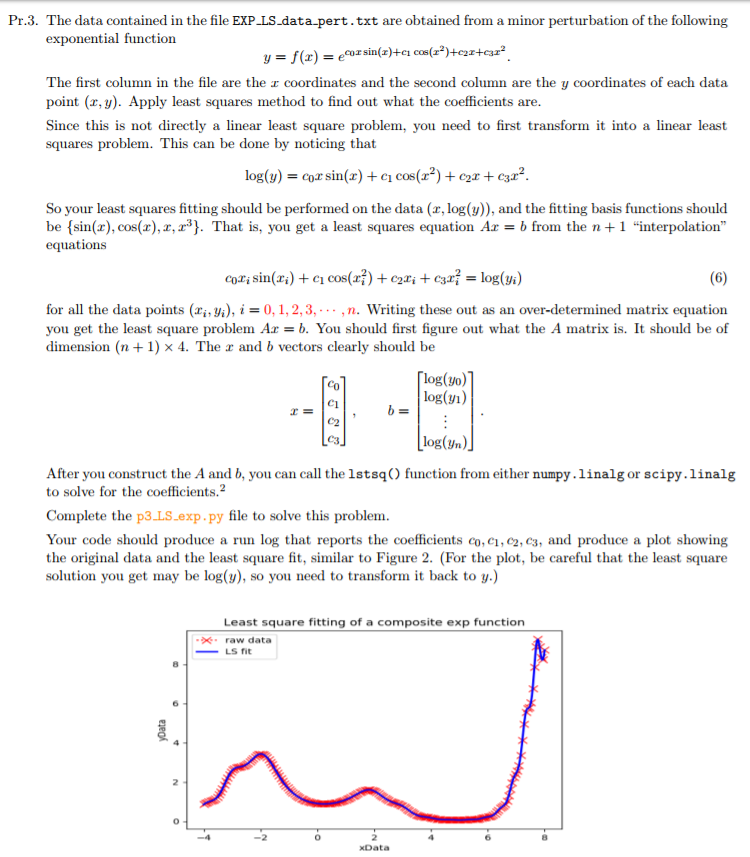
Pr.3. The data contained in the file EXP LS data-pert.txt are obtained from a minor perturbation of the following exponential function y = f(x) = ecoz sin(z)+C1 cos(12)-c22+caz2 The first column in the file are the z coordinates and the second column are the y coordinates of each data point (x, y). Apply least squares method to find out what the coefficients are Since this is not directly a linear least square proble, you need to first transform it into a linear least squares problem. This can be done by noticing that log(y)-cor sin(z) + ci cos(r') + c2x + cgz2 So your least squares fitting should be performed on the data (x, log(y)), and the fitting basis functions should be sin), cos(x),z,). That is, you get a least squares equation Ab from the n+1 "interpolation equations for all the data points (ri, vi),0,1,2,3, .. ,n. Writing these out as an over-determined matrix equation you get the least square problem Ab. You should first figure out what the A matrix is. It should be of dimension (n + 1) 4. The x and b vectors clearly should be Co C1 C2 C3 log(yo) b= | log(vi) log(yn) After you construct the A and b, you can call the 1stsq to solve for the coefficients.2 function from either numpy.linalg or scipy.linalg Complete the p3.LS exp.py file to solve this problem. Your code should produce a run log that reports the coefficients co,ci, c2, c3, and produce a plot showing the original data and the least square fit, similar to Figure 2. (For the plot, be careful that the least square solution you get may be log(y), so you need to transfor it back to y.) Least square fitting of a composite exp function >k. raw data LS fit 2 Pr.3. The data contained in the file EXP LS data-pert.txt are obtained from a minor perturbation of the following exponential function y = f(x) = ecoz sin(z)+C1 cos(12)-c22+caz2 The first column in the file are the z coordinates and the second column are the y coordinates of each data point (x, y). Apply least squares method to find out what the coefficients are Since this is not directly a linear least square proble, you need to first transform it into a linear least squares problem. This can be done by noticing that log(y)-cor sin(z) + ci cos(r') + c2x + cgz2 So your least squares fitting should be performed on the data (x, log(y)), and the fitting basis functions should be sin), cos(x),z,). That is, you get a least squares equation Ab from the n+1 "interpolation equations for all the data points (ri, vi),0,1,2,3, .. ,n. Writing these out as an over-determined matrix equation you get the least square problem Ab. You should first figure out what the A matrix is. It should be of dimension (n + 1) 4. The x and b vectors clearly should be Co C1 C2 C3 log(yo) b= | log(vi) log(yn) After you construct the A and b, you can call the 1stsq to solve for the coefficients.2 function from either numpy.linalg or scipy.linalg Complete the p3.LS exp.py file to solve this problem. Your code should produce a run log that reports the coefficients co,ci, c2, c3, and produce a plot showing the original data and the least square fit, similar to Figure 2. (For the plot, be careful that the least square solution you get may be log(y), so you need to transfor it back to y.) Least square fitting of a composite exp function >k. raw data LS fit 2