Could someone please check my work?

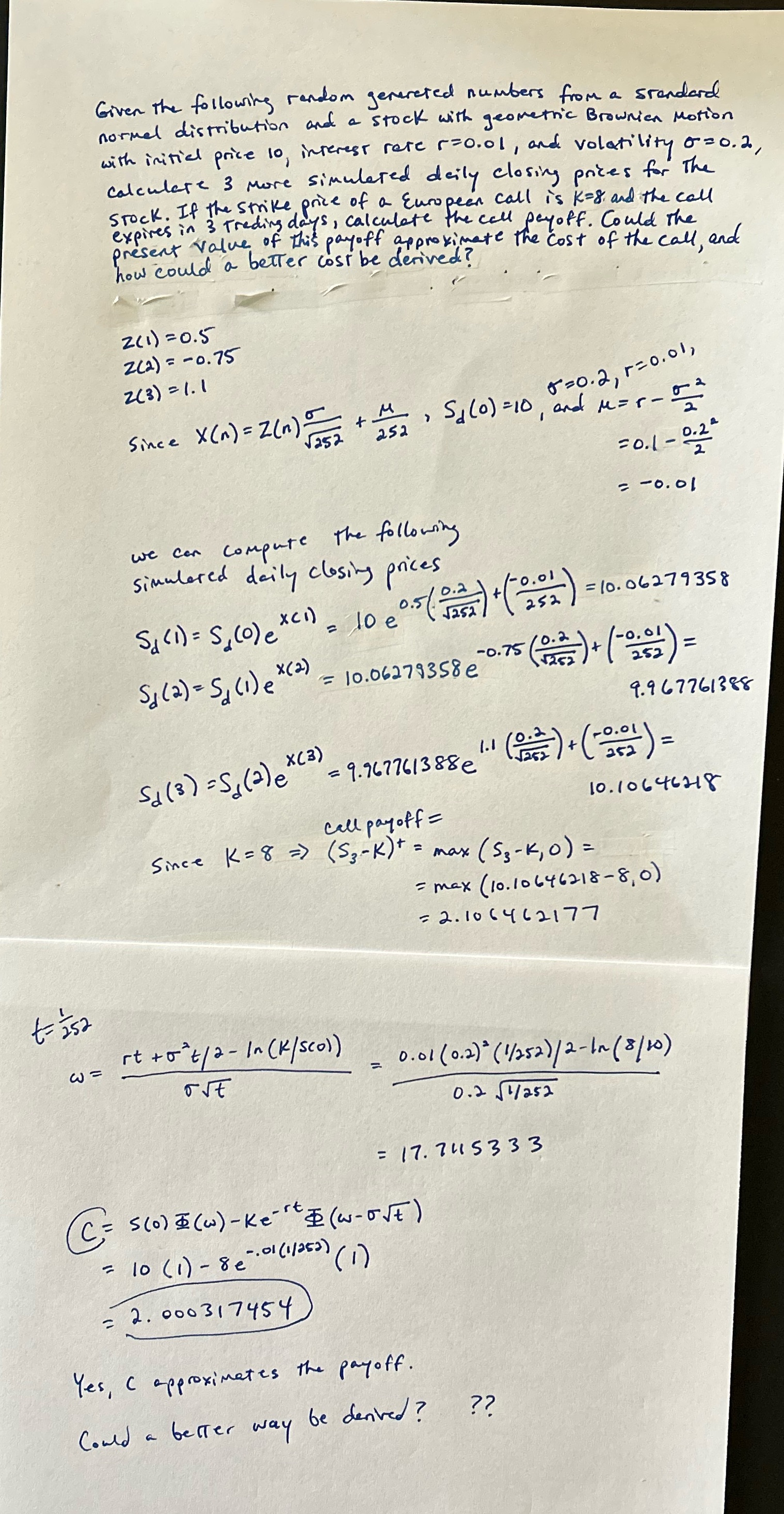
Given the following random generated numbers from a standard normal distribution and a stock with geometric Brownian Motion with initial price 10, interest rere rzo. ol, and volatility 0=0.2, calculare 3 more simulated daily closing prices for The STOCK. If the strike price of a European call is K=8 and the call expires in 3 Trading days, calculate the call payoff. Could The present Value of This payoff approximate the cost of the call, and how could a better cost be derived? 2(1 ) = 0.5 2 (2 ) = - 0.75 2 (3 ) = 1. 1 8 = 0 . 2 , 1 = 0 . ol , Since X ( n ) = Z (n ) + M , Sa(0) = 10, and Mar - 1252 252 =0.1 - 0.2 2 = -0. 01 we can compute the following simulared daily closing prices - 0.01 Sa ( 1) = S, (0)ex(")= 10 0.5 / 0.2 252 = 10. 06279 358 *(2) = 10.06279358 e - 0.75 Sa (2 ) = Slide 252 ) = 9.9 6 7761388 Sd ( 3 ) = S ( 2 ) @ * ( 3 ) "- = 9.967761388e 1.1 (0.2 + 0.01 = 10. 10646218 call pay off = Since K = 8 = ) ( 5 3 - K )+ = max ( S ; - k, 0 ) = = max ( 10. 10646218 - 8, 0) = 2. 10 (4 6 2177 t- 252 w = rt +0't/ 2 - In (k/sco)) - 0.01 ( 0.2 ) ( 1/252) / 2 - In ( 8/ 10) out 0.251/ 252 = 17. 74153 3 3 (C = 5 (0) E ( w ) -Ke" " E ( w- OVE ) = 10 ( 1) - 8e--01(1/252) ( 1 ) = 2. 000 317454 Yes, C approximates the payoff. Could a better way be derived