could someone please help me with these problems.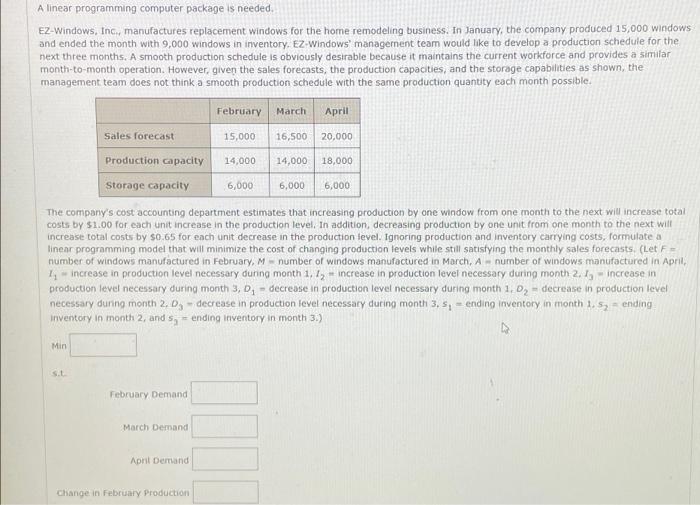

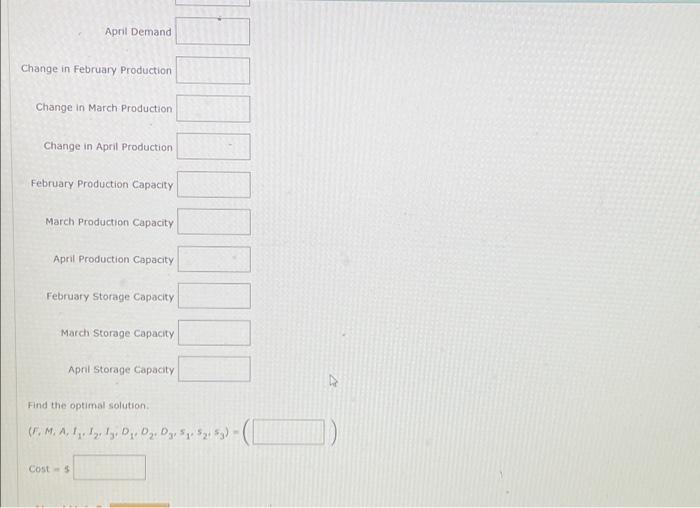
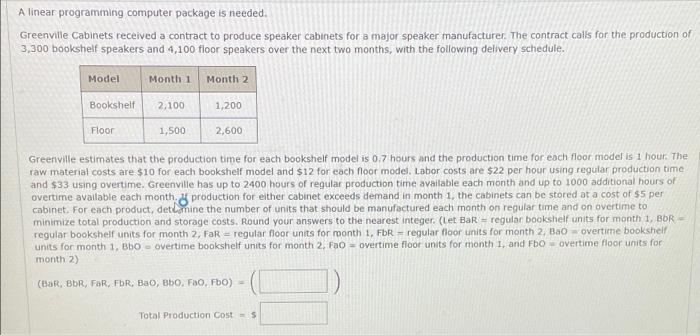
A linear programming computer package is needed. EZ-Windows, Inc., manufactures replacement windows for the home remodeling business. In January, the company produced 15,000 windows and ended the month with 9,000 windows in inventory. EZ-Windows' management team would like to develop a production schedule for the next three months. A smooth production schedule is obviously desirable because it maintains the current workforce and provides a similar month-to-month operation. However, given the sales forecasts, the production capacities, and the storage capabilities as shown, the management team does not think a smooth production schedule with the same production quantity each month possible. February March 15,000 16,500 Production capacity 14,000 14,000 18,000 Storage capacity 6,000 The company's cost accounting department estimates that increasing production by one window from one month to the next will increase total costs by $1.00 for each unit increase in the production level. In addition, decreasing production by one unit from one month to the next will increase total costs by $0.65 for each unit decrease in the production level. Ignoring production and inventory carrying costs, formulate a linear programming model that will minimize the cost of changing production levels while still satisfying the monthly sales forecasts. (Let F= number of windows manufactured in February, M number of windows manufactured in March, A number of windows manufactured in April, 1-increase in production level necessary during month 1, 1, increase in production level necessary during month 2. I, increase in production level necessary during month 3, D decrease in production level necessary during month 1, D decrease in production level necessary during month 2. Da decrease in production level necessary during month 3, 5, ending inventory in month 1. Sending inventory in month 2, and sending Inventory in month 3.) 4 Min s.t. Sales forecast February Demand March Demand April Demand Change in February Production April 6,000 20,000 6,000 April Demand Change in February Production Change in March Production. Change in April Production. February Production Capacity March Production Capacity: April Production Capacity February Storage Capacity March Storage Capacity April Storage Capacity Find the optimal solution. (F. M. A. 1. 12. 1, D, D, D3, S S2 S3) - Cost-$ A linear programming computer package is needed. Greenville Cabinets received a contract to produce speaker cabinets for a major speaker manufacturer. The contract calls for the production of 3,300 bookshelf speakers and 4,100 floor speakers over the next two months, with the following delivery schedule. Model Bookshelf Floor Month 1 Month 2 2,100 1,500 1,200 2,600 Greenville estimates that the production time for each bookshelf model is 0.7 hours and the production time for each floor model is 1 hour. The raw material costs are $10 for each bookshelf model and $12 for each floor model. Labor costs are $22 per hour using regular production time and $33 using overtime. Greenville has up to 2400 hours of regular production time available each month and up to 1000 additional hours of overtime available each month, production for either cabinet exceeds demand in month 1, the cabinets can be stored at a cost of $5 per cabinet. For each product, detamine the number of units that should be manufactured each month on regular time and on overtime to minimize total production and storage costs. Round your answers to the nearest integer. (Let BaR= regular bookshelf units for month 1, BbR- regular bookshelf units for month 2, FaR= regular floor units for month 1, FbR regular floor units for month 2, Bao overtime bookshelf units for month 1, Bb0- overtime bookshelf units for month 2, FaO = overtime floor units for month 1, and Fb0 overtime floor units for month 2) (BaR, BbR, FaR, FbR, Bao, Bb0. Fao, Fb0) - Total Production Cost S