could you give me explanations on this statistics problem ? I am stuck, and I do need your help. Thanks

please refer to the example and materials I gave.

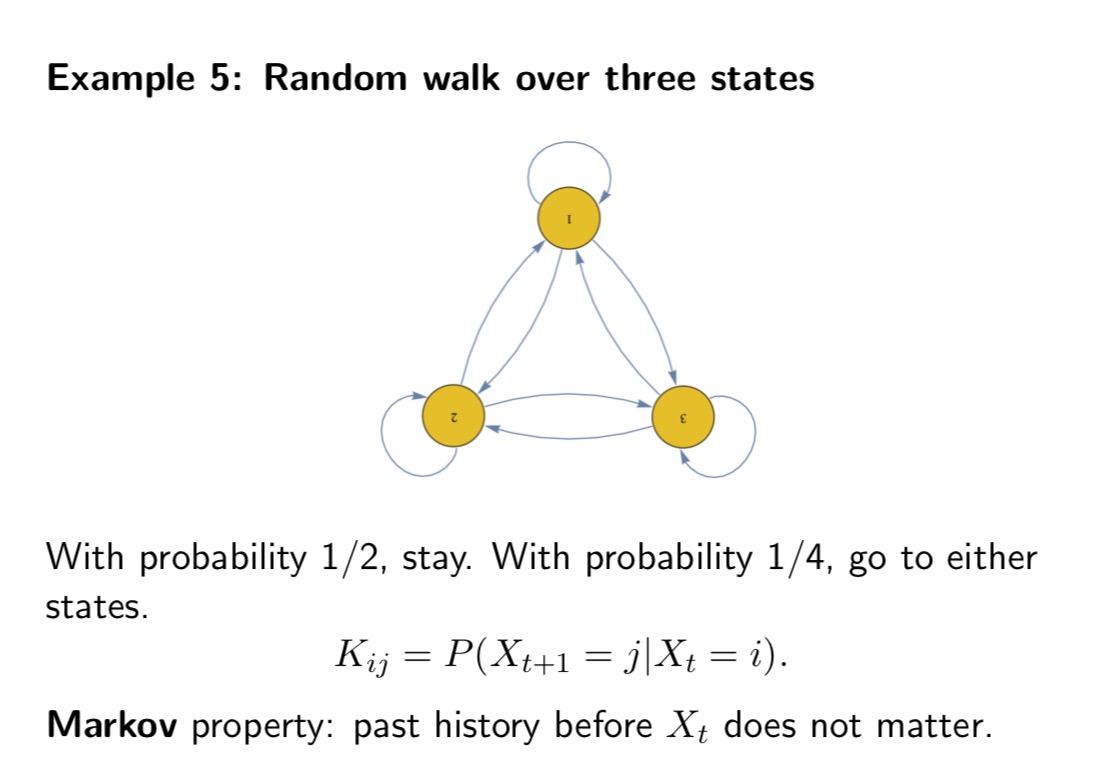
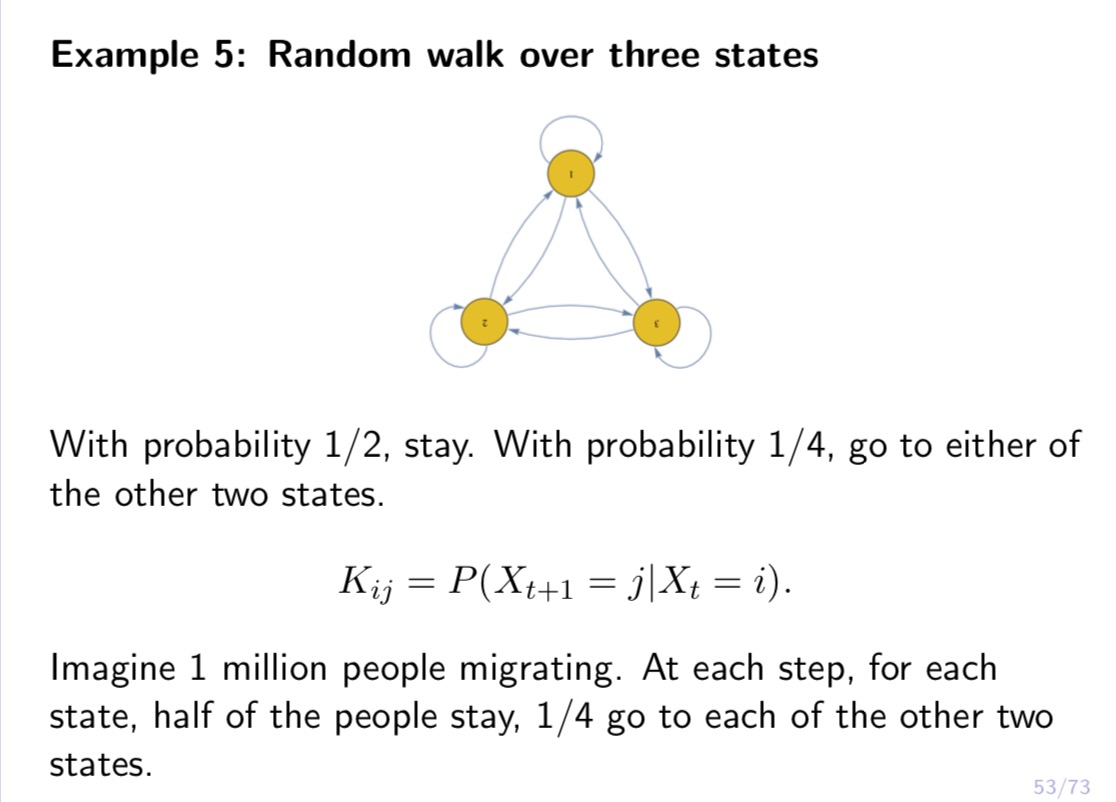
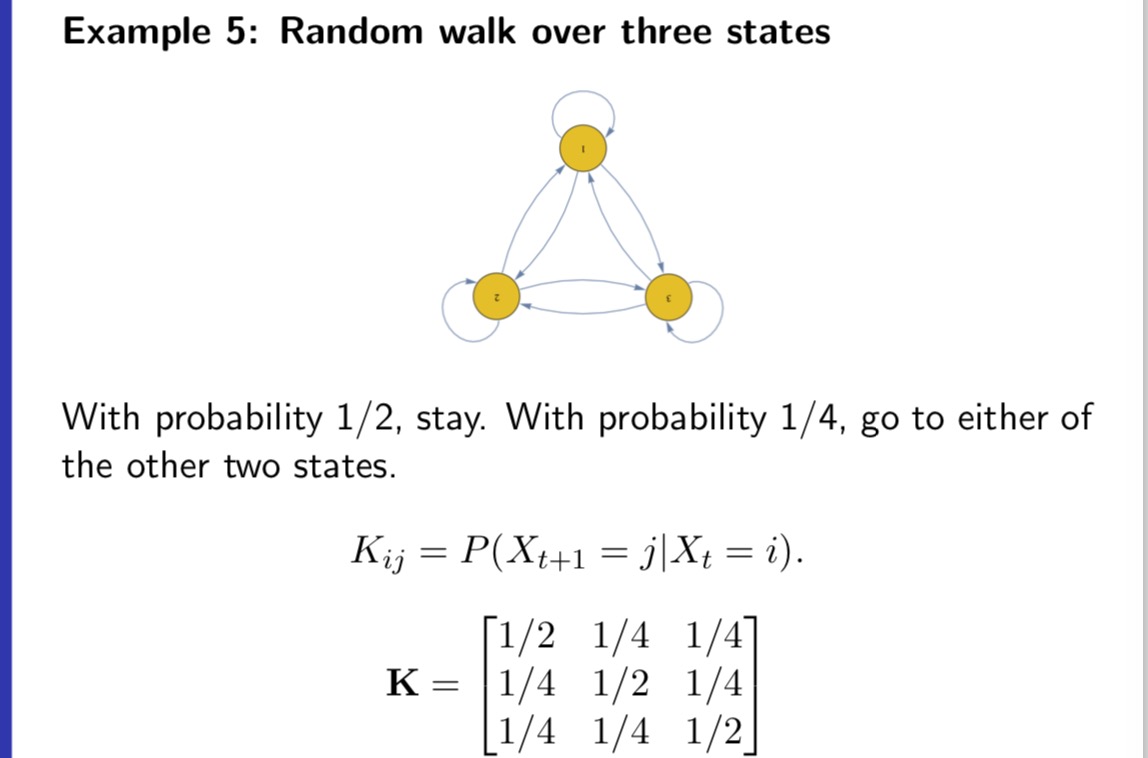
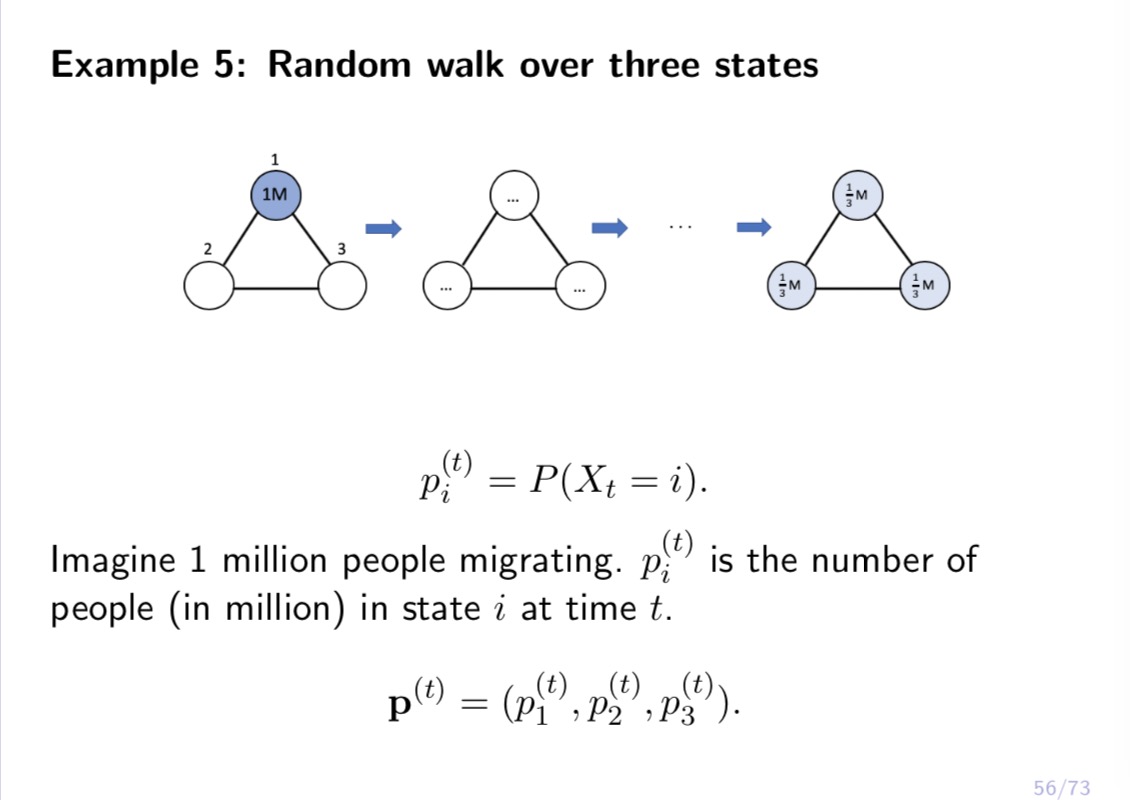
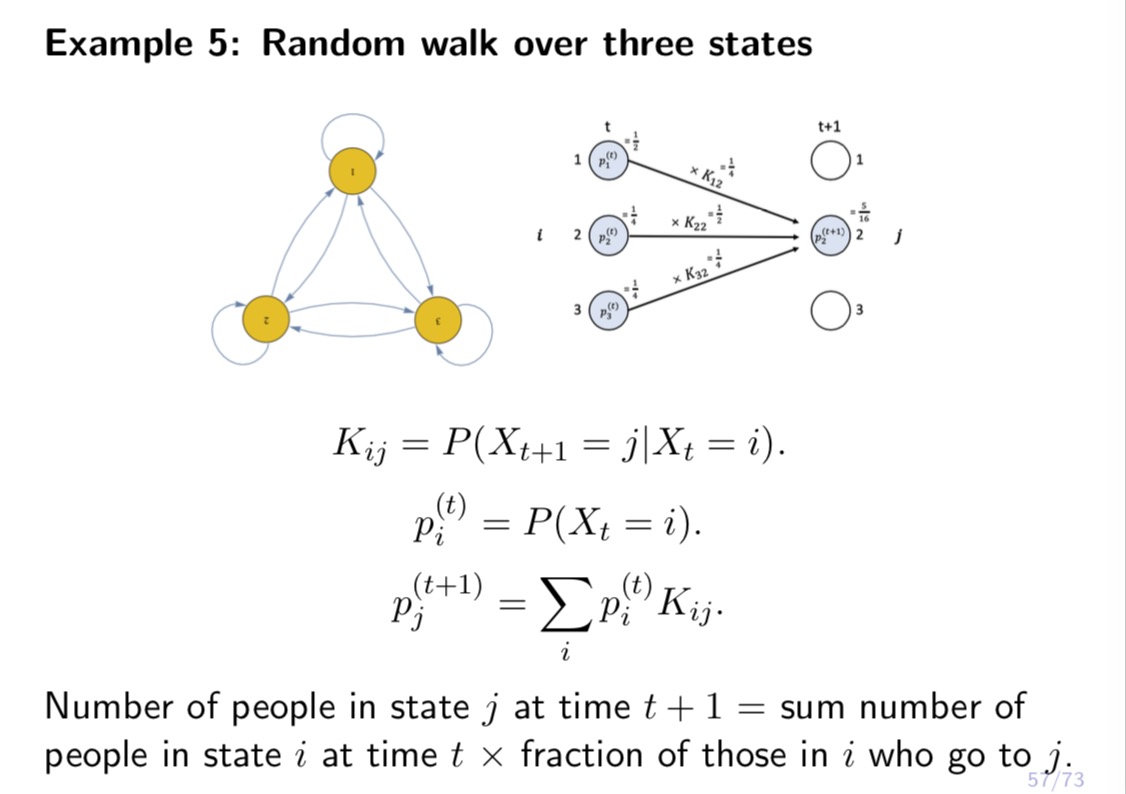
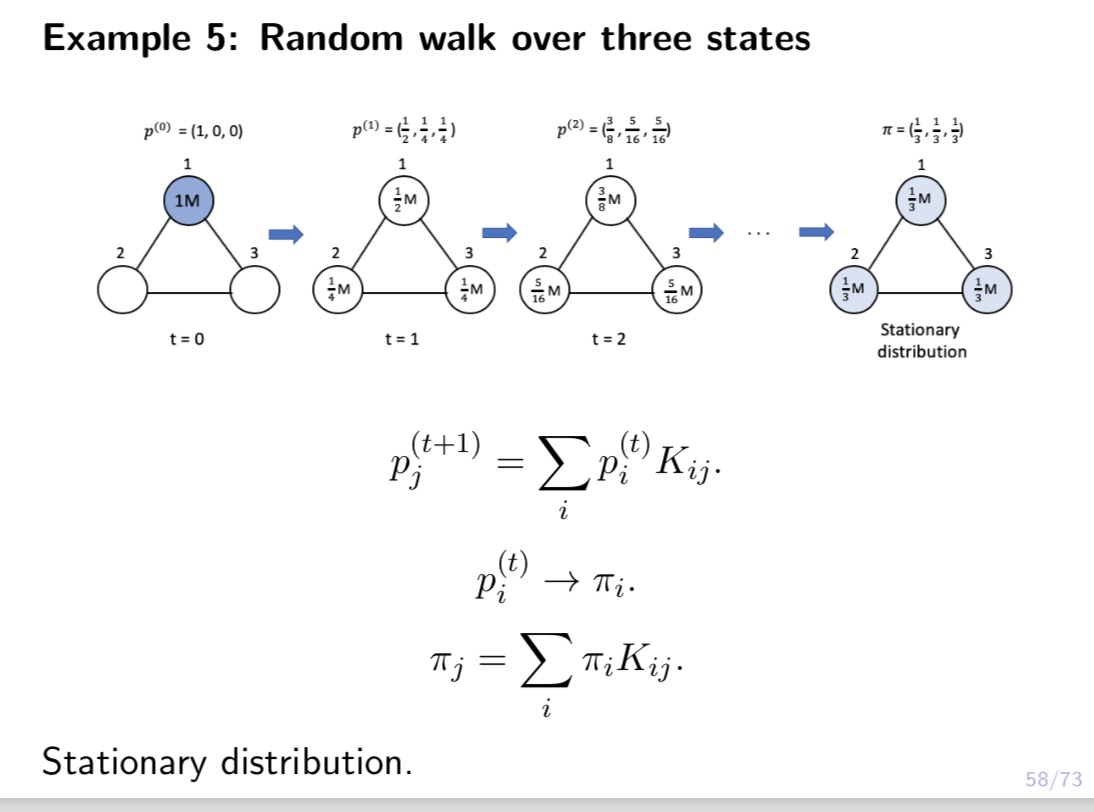
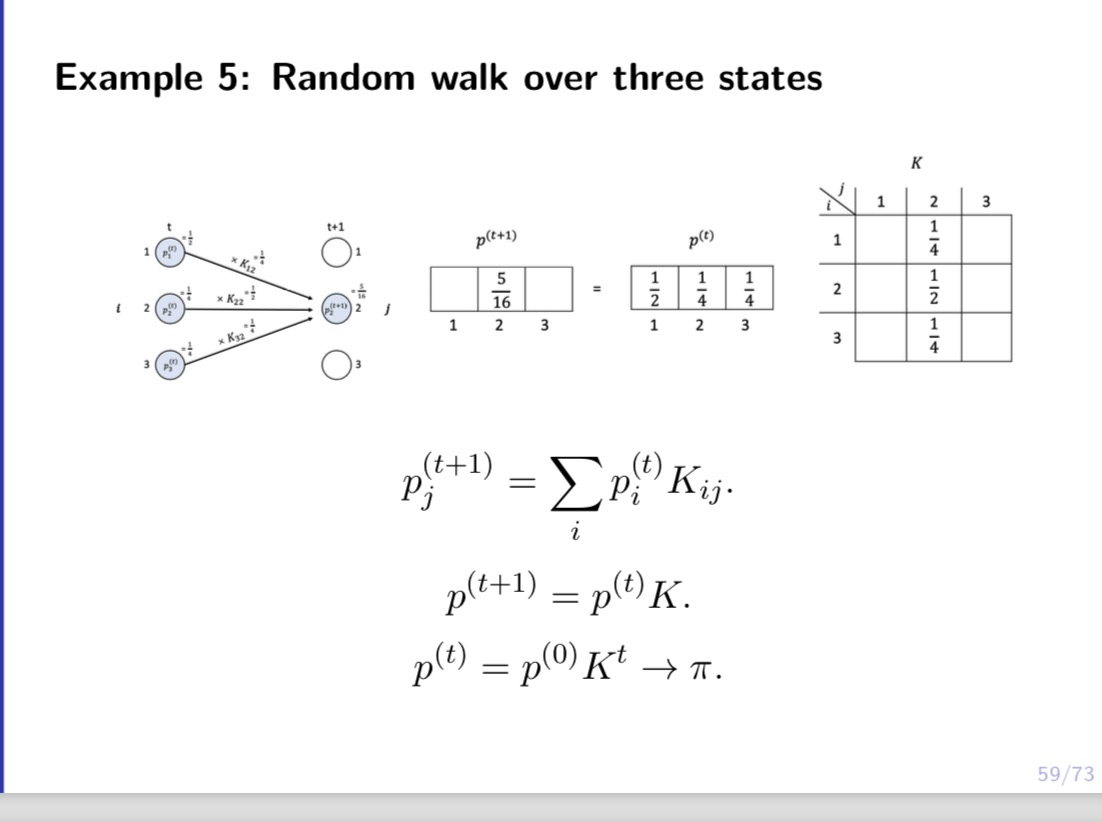
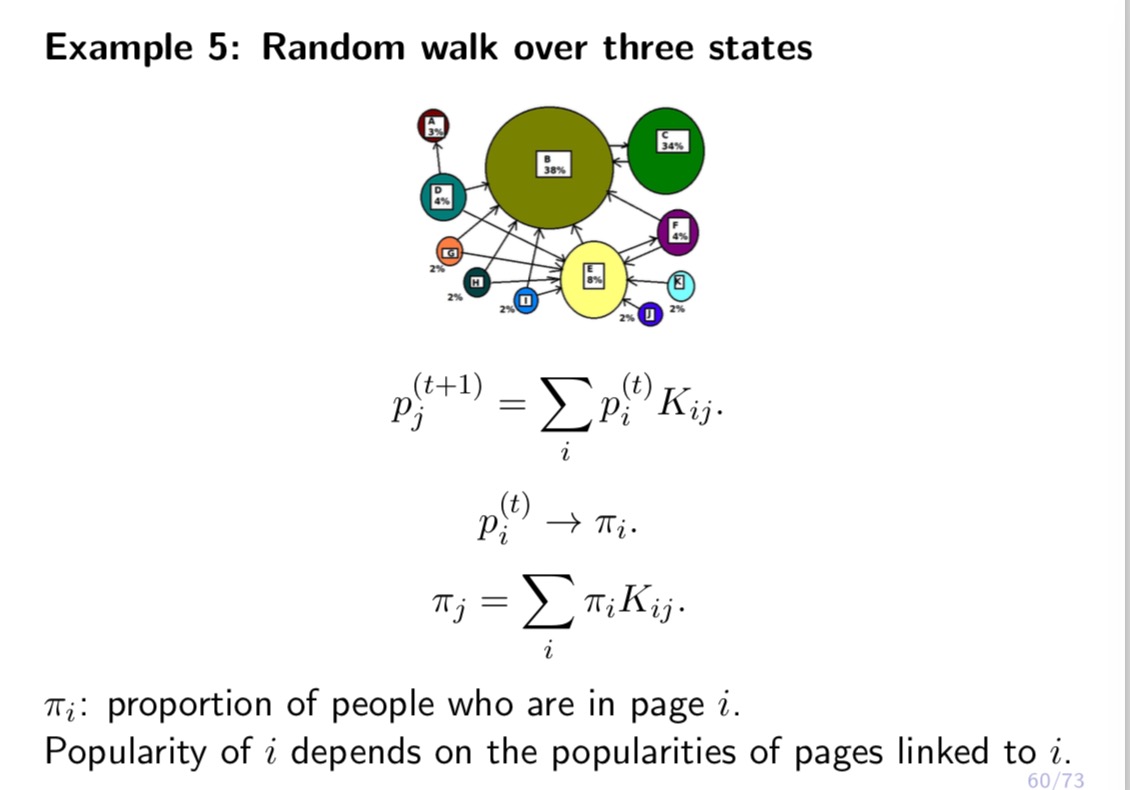
Consider a random walk over 3 webpages, 1, 2, 3. At any step, if the person is at webpage 1, then with probability 1 / 6, she will go to webpage 2, and with probability 1/6, she will go to webpage 3. If the person is at webpage 2, then with probability 1 / 2, she will go to webpage 1, and with probability 1 / 2, she will go to webpage 3. If the person is at webpage 3, then with probability 1 / 2, she will go to webpage 1, and with probability 1/2, she will go to webpage 2. Let X, be the webpage the person is browsing at time t, and let us assume she starts from webpage 1 at time 0, i.e., X0 = 1. (1) Let Ki,- = P(Xt+1 = j|Xt = 2'). Let K = (Kij) be the 3 x 3 transition matrix. Write down K. (2) Let p?) = P(Xt = 2'). Let pm = (1?)an = 1,2,3) be the row vector. Calculate pm for = 1, 2, 3. Using concrete numbers, explain 10(2) = p(1)K. (3) Let 7r,- be the stationary distribution at webpage 'i, so that 7r, = 2;, 7r,-K,-j. Let 7r = (17,-,1' = 1, 2, 3) be the row vector. Then 7r = WK. Given K, solve 7r from this equation. Is 13(3) close to 1r? (4) Based on the above calculations, answer the following questions. Suppose there are 1 million people doing the above random walk independently, and suppose they all start om webpage 1 at time t = 0. Then on average, what is the distribution of these 1 million people for t = 1, 2, 3? What is the stationary distribution of these 1 million people? Which page is the most popular? Example 5: Random walk over three states With probability 1/2, stay. With probability 1/4, go to either states. Kij = P(Xt+1 = ]]Xt = i). Markov property: past history before Xt does not matter.Example 5: Random walk over three states With probability 1/ 2, stay. With probability 1/4, go to either of the other two states. Kz-j = Pug;+1 = let = 7:). Imagine 1 million people migrating. At each step, for each state, half of the people stay, 1/4 go to each of the other two states. - 5.3 {3 Example 5: Random walk over three states With probability 1/2, stay. With probability 1/4, go to either of the other two states. K13. = P(Xt+1 = let = 4). 1/2 1/4 1/4 K: 1/4 1/2 1/4 i1/4 1/4 1/2] Example 5: Random walk over three states I U \"9 With probability 1/2, stay. With probability 1/4, go to either of the other two states. K4; = 19(X15+1 = j|Xt = i). pf) = P(Xt = 7:). Imagine 1 million people migrating. p?) is the number of people (in million) in statei at time t. p\") = (aw???)- 55 F3 Example 5: Random walk over three states 1M SM 3 Pi (t ) = P(Xt = i). Imagine 1 million people migrating. p;" is the number of people (in million) in state i at time t. p(t) = (p1 , p2 , P3 56/73Example 5: Random walk over three states Number of people in state 3' at time t+ 1 = sum number of people in state 3' at time t x fraction of those in 3' who go towj Example 5: Random walk over three states 5 pm =t1,o,0} pm ={..1 PIZ}=I;.;.;} E={;.5.;] Stationary distribution Stationary distribution. 58 73 \fExample 5: Random walk over three states 713: E 713K\". 1', 713: proportion of people who are in page 3'. Popularity of 2' depends on the popularities of pages linked to 22. E10 ' T3