Could you please help me to answer this question?

4. Estimating the inputs using the Black-Scholes option pricing model in the options analysis of the investment timing option

Option analysis involves gathering significant amounts of information, synthesizing the data, and using the data in models applied in options analysis.

Consider the case of RTE Com Inc.:

RTE Com Inc. is considering a project for a new cloud-based online storage system for companies and individuals to back up their data. The cost of the project is $55 million, but the future cash flows depend on how this new cloud-based online storage will compete with existing companies that offer online data backup.

The company believes that this project has a strong selling feature but is uncertain that it would earn cash flows as projected. The team proposing this project has come up with the following data:

Demand . Probability . Annual Cash Flow

High . 0.40 . $50 million

Average . 0.40 . $35 million

Low . 0.20 . $15 million

Project's cost of capital . 13%

Life of project . Three years

52-week Treasury note . 5%

• The project team also noted that the company has an option to wait for one year in order to see its competitors' positions and observe how the market responds. This will help in getting more information about market demand and in figuring out which set of cash flows will occur.

• Analysts used different approaches to evaluate the project, but the management team insists that the Black-Scholes option pricing model (OPM) will help them make a more informed decision. The model requires five inputs: (1) the risk-free rate; (2) the time until the option expires; (3) the strike price; (4) the current price of the stock, which in this case would be a proxy for the value of the underlying asset; and (5) the variance of the project's expected return.

• You need to calculate both the value of the underlying asset in the project and its rate of return. For RTE Com Inc., the underlying asset is the project itself. The current value of the project will be the_________________ ( Present or Future)value of its expected cash flows.

_ Based on the data given, calculate the value of the project, its return, and the standard deviation of the returns (using the direct method) if the company decides to wait for a year. (Cash flow values in the table are in millions. Round your answers to two decimal places).

Note : ( red arrows can show up to you answers inside the blank) ex/ Number 1 in red color that means you can see down number 1 with multiple choices inside the blank

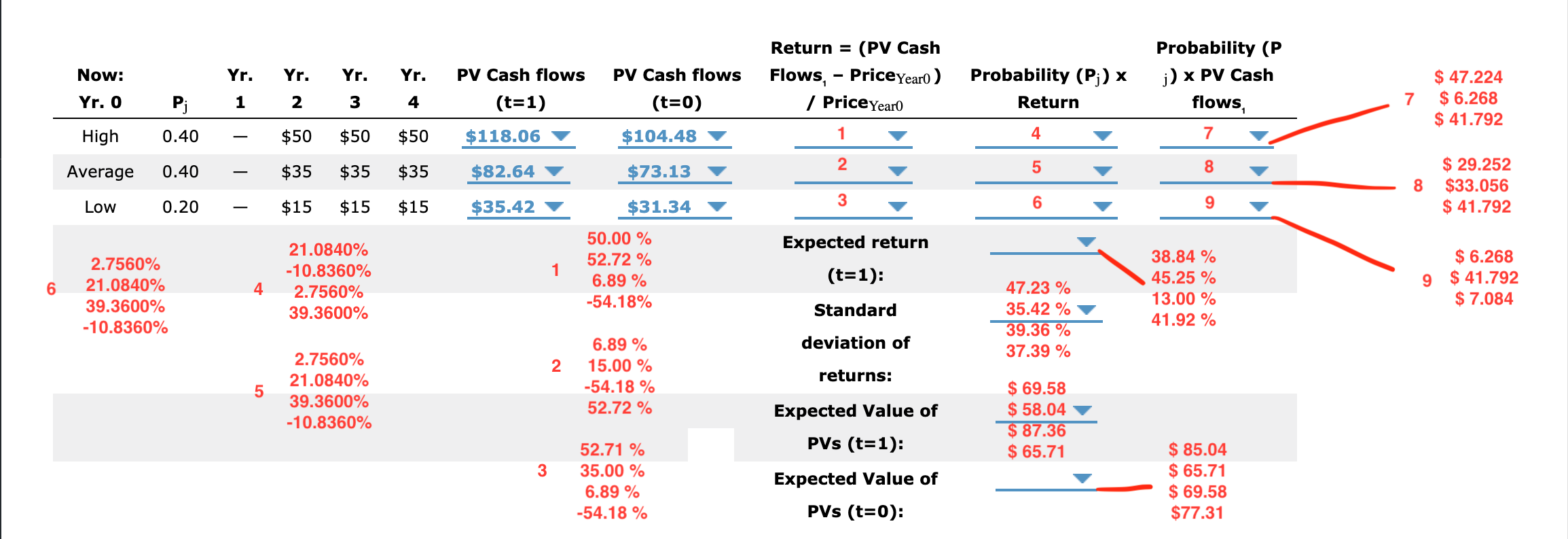
Return = (PV Cash Probability (P Now: Yr. Yr. Yr. Yr. PV Cash flows PV Cash flows Flows, - PriceYear0 ) Probability (P;) x j) x PV Cash $ 47.224 Yr. 0 Pi 1 2 3 4 (t=1) (t=0) / PriceYear0 Return flows 7 $ 6.268 $ 41.792 High 0.40 $50 $50 $50 $118.06 $104.48 4 7 Average 0.40 $35 $35 $35 $82.64 $73.13 2 5 8 $ 29.252 8 $33.056 Low 0.20 $15 $15 $15 $35.42 $31.34 3 6 9 $ 41.792 21.0840% 50.00 % Expected return 52.72 % 38.84 % $ 6.268 2.7560% -10.8360% 1 21.0840% 6.89 % (t=1): $ 41.792 6 4 2.7560% 47.23 % 45.25 % 9 39.3600% -54.18% 13.00 % $ 7.084 39.3600% Standard 35.42 % 39.36 % 41.92 % -10.8360% 6.89 % deviation of 2.7560% 37.39 % 2 15.00 % 21.0840% returns: 5 -54.18 % $ 69.58 39.3600% 52.72 % Expected Value of $ 58.04 -10.8360% $ 87.36 52.71 % PVs (t=1): $ 65.71 $ 85.04 3 35.00 % Expected Value of $ 65.71 6.89% $ 69.58 -54.18 % PVs (t=0): $77.311 aawwa 2 = Risk-Free Interest Rate = Time until Option Expires = Cost to Implement the Project = Current Value of the Project = Variance of the Project's Rate of Return = Cumulative Normal Distribution Function of (11 = Cumulative Normal Distribution Function of d; aawwa = RiskFree Interest Rate = Time until Option Expires = Cost to Implement the Project = Current Value of the Project = Variance of the Project's Rate of Return = Cumulative Normal Distribution Function of (11 ) + [mm + (072)]t} / (0115)) ll 2 9- I 4 V = Cumulative Normal Distribution Function of d2