Could you please help me with this

Question 1:

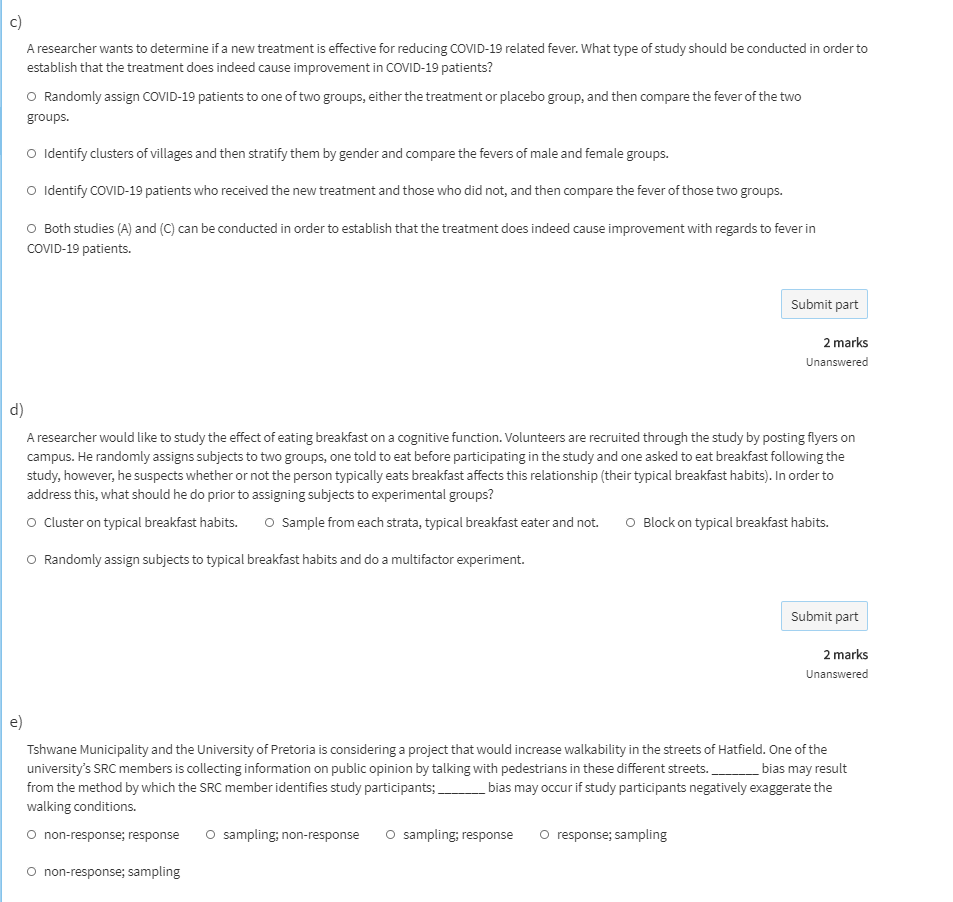
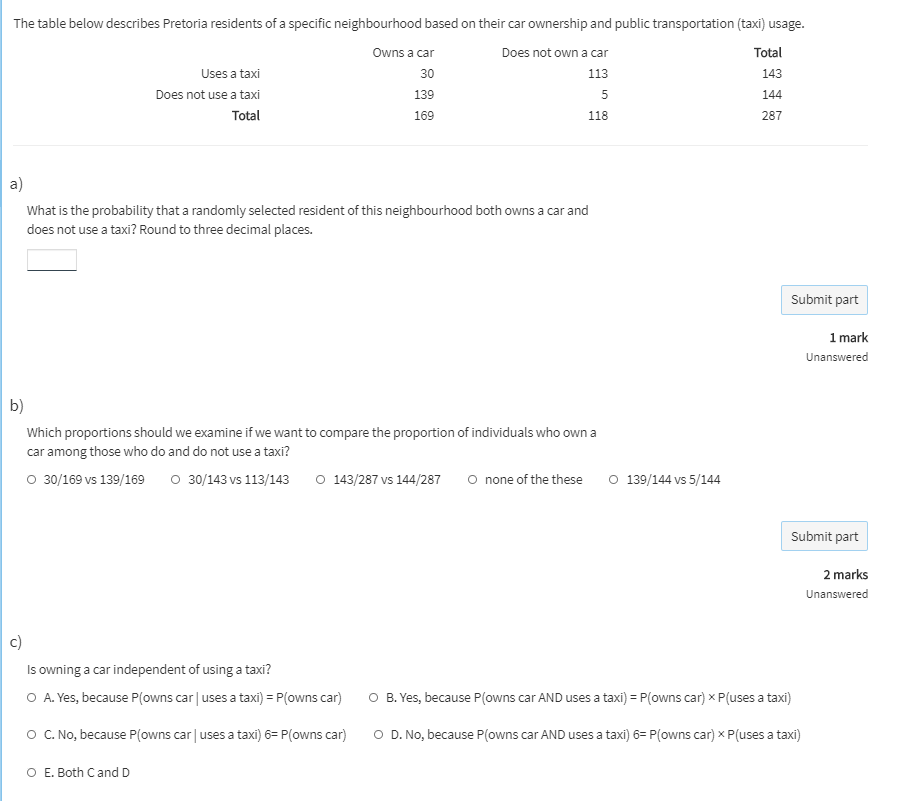
Multiple Choice Questions: a) A comprehensive survey released by a university reports that the true proportion of all students at the university who smoke is 0.40. You survey 100 students in your residence and record that the proportion of students who smoke is 0.25. The proportion of all students at the university who smoke is a and the proportion of students who smoke in your residence is a O parameter; statistic O statistic; parameter O population; sample O none of these O measure of central tendency; measure of variability Submit part 2 marks Unanswered b) The plot below displays the distribution of the percent of hours spent sleeping per day by students in residents at the University of Pretoria. Which of the following are valid estimates of the mean and median of this distribution? Percent in 0.3 0.4 0.5 0.6 0.7 0.8 Percent of hours spent sleeping O mean = 0.35, median = 0.40 O mean = 0.4, median = 0.4 O mean = 0.40, median = 0.45 O mean = 0.45, median = 0.40 Submit part 2 marks Unansweredc) A researcher wants to determine if a new treatment is effective for reducing COVID-19 related fever. What type of study should be conducted in order to establish that the treatment does indeed cause improvement in COVID-19 patients? O Randomly assign COVID-19 patients to one of two groups, either the treatment or placebo group, and then compare the fever of the two groups. O Identify clusters of villages and then stratify them by gender and compare the fevers of male and female groups. O Identify COVID-19 patients who received the new treatment and those who did not, and then compare the fever of those two groups. O Both studies (A) and (C) can be conducted in order to establish that the treatment does indeed cause improvement with regards to fever in COVID-19 patients. Submit part 2 marks Unanswered d) A researcher would like to study the effect of eating breakfast on a cognitive function. Volunteers are recruited through the study by posting flyers on campus. He randomly assigns subjects to two groups, one told to eat before participating in the study and one asked to eat breakfast following the study, however, he suspects whether or not the person typically eats breakfast affects this relationship (their typical breakfast habits). In order to address this, what should he do prior to assigning subjects to experimental groups? O Cluster on typical breakfast habits. O Sample from each strata, typical breakfast eater and not. O Block on typical breakfast habits. O Randomly assign subjects to typical breakfast habits and do a multifactor experiment. Submit part 2 marks Unanswered e) Tshwane Municipality and the University of Pretoria is considering a project that would increase walkability in the streets of Hatfield. One of the university's SRC members is collecting information on public opinion by talking with pedestrians in these different streets. bias may result from the method by which the SRC member identifies study participants; bias may occur if study participants negatively exaggerate the walking conditions. O non-response; response O sampling; non-response O sampling; response O response; sampling O non-response; samplingf) An engineering student is playing an online computer game with friends. He thinks he is very skilled and that he has a better chance of winning than a random chance, so he estimated that his probability of winning an individual online game is 0.45. Assuming that each online game played is independent of the other onine games, the student says that his probability of winning both games is 0.9. What is the best assessment of this statement? O This is an incorrect probability calculation because the engineering student did not use the normal distribution. O This is a correct probability calculation because the engineering student just adds the probability of winning each online game. O This is an incorrect probability calculation because the engineering student should have multiplied the probability of winning each online game. O This is an incorrect probability calculation because the engineering student should have used the formula P(A or B) = P(A) + P(B) - P(A and B).The table below describes Pretoria residents of a specific neighbourhood based on their car ownership and public transportation (taxi) usage. Owns a car Does not own a car Total Uses a taxi 30 113 143 Does not use a taxi 139 144 Total 169 118 287 a) What is the probability that a randomly selected resident of this neighbourhood both owns a car and does not use a taxi? Round to three decimal places. Submit part 1 mark Unanswered b) Which proportions should we examine if we want to compare the proportion of individuals who own a car among those who do and do not use a taxi? 30/169 vs 139/169 O 30/143 vs 113/143 O 143/287 vs 144/287 O none of the these O 139/144 vs 5/144 Submit part 2 marks Unanswered c) Is owning a car independent of using a taxi? O A. Yes, because P(owns car | uses a taxi) = P(owns car) O B. Yes, because P(owns car AND uses a taxi) = P(owns car) x P(uses a taxi) O C. No, because P(owns car | uses a taxi) 6= P(owns car) O D. No, because P(owns car AND uses a taxi) 6= P(owns car) x P(uses a taxi) O E. Both C and D