Could you please solve and explain this question to me clearly?

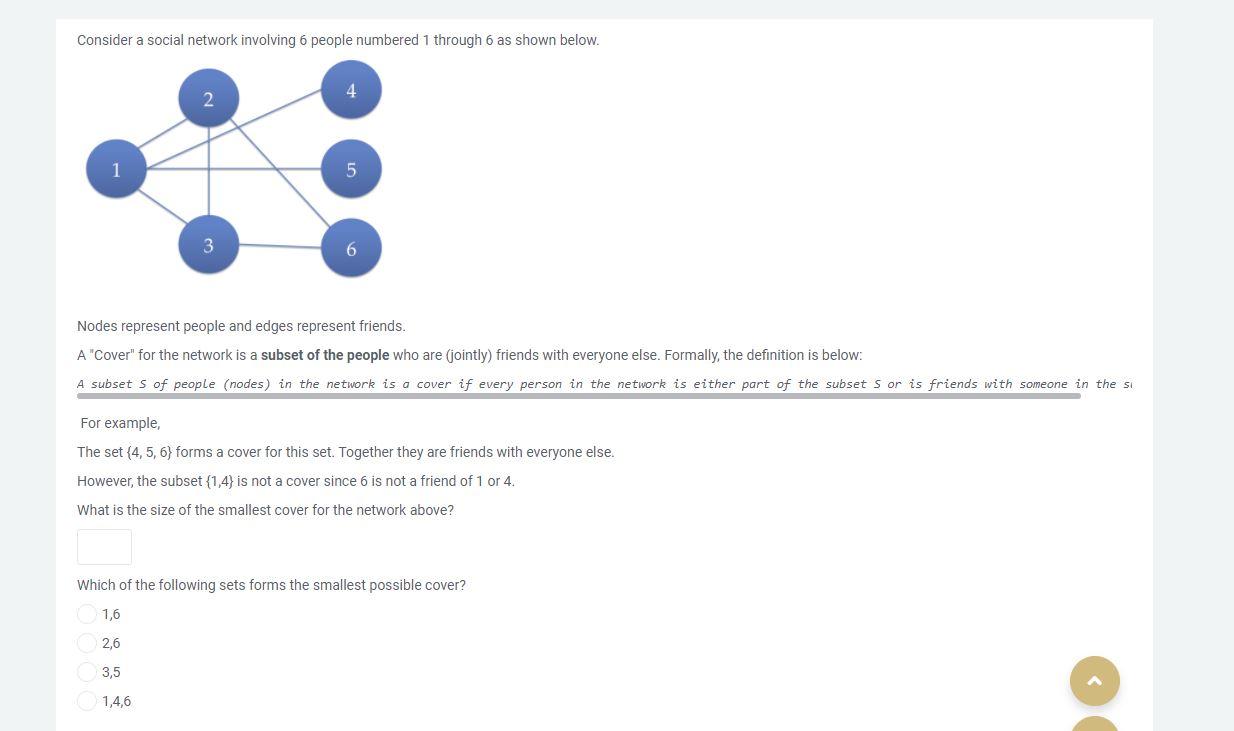
Consider a social network involving 6 people numbered 1 through 6 as shown below. 1 3 Nodes represent people and edges represent friends. A "Cover" for the network is a subset of the people who are (jointly) friends with everyone else. Formally, the definition is below: A subset s of people (nodes) in the network is a cover if every person in the network is either part of the subset sor is friends with someone in the si For example, The set {4, 5, 6} forms a cover for this set. Together they are friends with everyone else. However, the subset (1,4) is not a cover since 6 is not a friend of 1 or 4 What is the size of the smallest cover for the network above? Which of the following sets forms the smallest possible cover? 1,6 2,6 3,5 1,4,6 Consider the following simple Greedy Cover Algorithm: 1. Pick the person with maximum number of friends in the network, add them to the cover. 2. Delete this person and their friends from the network. 3. Repeat step 1 until no people remain. According to the algorithm, what is the id of the first person picked to belong to the cover? What is true of the remaining network after node id 1 and its friends are deleted? Only 6 remains in the network Nothing remains Only two nodes 4,5 remain Only 5 remains in the network 2,3,4,5,6 remain What is the size of the smallest cover discovered by the greedy algorithm for the network above