Course name : Design and Analysis or Algorithm

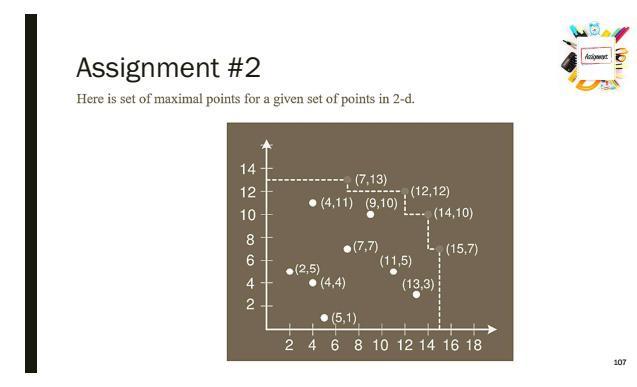
Assignment #2 Assignment Find the Time Complexity of two algorithms given in next slides. Both the algorithms solve the same problem. Remember that sorting takes (n.log n) time. Also compare the time complexity of both the algorithms. Date: - Date: Sunday, 31 December, 2020 before 23:55 HRS Groups up to 4 students are allowed, but not mandatory. 104 Aw ou Assignment #2 Suppose you want to buy a car. You want the pick the fastest car. But fast cars are expensive, you want the cheapest. You cannot decide which is more important: speed or price. Definitely you do not want a car if there is another that is both faster and cheaper. We say that the fast, cheap car dominates the slow, expensive car relative to your selection criteria. So, given a collection of cars, we want to list those cars that are not dominated by any other. Here is how we might model this as a formal problem. Let a point p in 2-dimensional space be given by its integer coordinates, p = (p.x, p.y). A point p is said to be dominated by point q if p.x sq.x and pys 9.y. Given a set of n points, P = {p.1.P2...., pp) in 2-space a point is said to be maximal if it is not dominated by any other point in P. 105 Awt (11 Assignment #2 The car selection problem can be modelled this way: For each car we associate (x, y) pair where x is the speed of the car and y is the negation of the price. High y value means a cheap car and low y means expensive car. Think of y as the money left in your pocket after you have paid for the car. Maximal points correspond to the fastest and cheapest cars. The 2-dimensional Maxima is thus defined as Given a set of points P = {p.P2..... P.} in 2-space, output the set of maxim al points of P. i.e., those points pisuch that p; is not dominated by any other point of P. 106 Assignment #2 Aignet Algo#1 MAXIMA(int n, Point P[1...n)) 1 for i 1 ton 2 do maximal true 3 for 1 ton 4 do 5 if (i #j) and (P[i].x