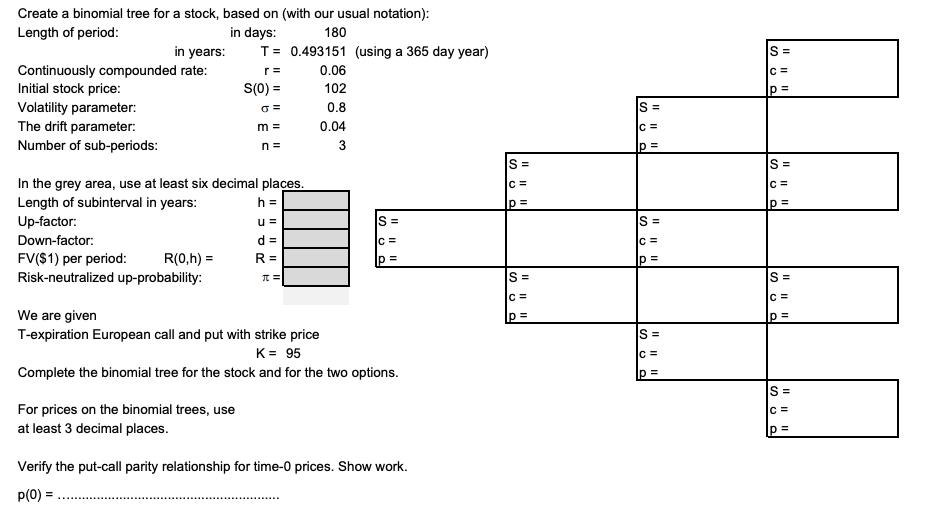
Create a binomial tree for a stock, based on (with our usual notation): Length of period: 180 in years: Continuously compounded rate: Initial stock price: Volatility parameter: The drift parameter: Number of sub-periods: in days: FV($1) per period: R(0,h) = Risk-neutralized up-probability: T = 0.493151 (using a 365 day year) r= S(0) = For prices on the binomial trees, use at least 3 decimal places. G= In the grey area, use at least six decimal places. Length of subinterval in years: h = Up-factor: u = Down-factor: d = R= = m= n = 0.06 102 0.8 0.04 3 S= C= p= We are given T-expiration European call and put with strike price K = 95 Complete the binomial tree for the stock and for the two options. Verify the put-call parity relationship for time-0 prices. Show work. p(0) = ..... S= C= p= |S= C= p= S= C= p= S= C= p= S= C = p= S= C= p= S= S || || || C= p= S= C= p= S= C= p=