Create a class called polynomial for performing arithmetic with polynomials. The class can be used to add, subtract, multiply, divide, finds the remainder of two polynomials.

Download the needed files from the blackboard and implement the missing functions.

// polynomial.h

#include

#include

using namespace std;

class polynomial

{

friend ostream& operator

friend istream& operator>>(istream& isObject, polynomial& cObject);

public:

void set(int, double*);

int getDegree() const;

double* getPointer() const;

polynomial operator+(const polynomial&) const;

polynomial operator-(const polynomial&) const;

polynomial operator*(const polynomial&) const;

polynomial operator/(const polynomial&) const;

polynomial operator%(const polynomial&) const;

polynomial& operator=(const polynomial&);

polynomial(const polynomial &otherObject);

polynomial(int, double*);

polynomial();

~polynomial();

private:

int degree;

double *p;

};

// polynomialImp.cpp

#include

#include "polynomial.h"

{

degree = nDegree;

p = new double[degree+1];

assert(p != NULL);

for(int i=0; i

p[i] = q[i];

}

int polynomial::getDegree() const

{

return degree;

}

double* polynomial::getPointer() const

{

return p;

}

polynomial& polynomial::operator=(const polynomial &pObject)

{

}

polynomial polynomial::operator+(const polynomial &pObject) const

{

}

polynomial polynomial::operator-(const polynomial &pObject) const

{

}

polynomial polynomial::operator*(const polynomial &pObject) const

{

}

polynomial polynomial::operator/(const polynomial &pObject) const

{

}

polynomial polynomial::operator%(const polynomial &pObject) const

{

}

polynomial::polynomial(int nDegree, double *q)

{

set(nDegree, q);

}

polynomial::polynomial(const polynomial &pObject )

{

}

polynomial::polynomial()

{

degree = 0;

p = new double[degree+1];

assert(p != NULL);

p[0] = 0;

}

polynomial::~polynomial()

{

delete [] p;

p = NULL;

}

ostream& operator

{

}

istream& operator>>(istream& isObject, polynomial& cObject)

{

}

// polynomial.cpp

#include "polynomial.h"

void printMenu();

int main()

{

polynomial poly1, poly2;

polynomial polyAdd, polySub, polyMult, polyDiv, polyRemainder;

int selection = 0;

cin >> poly1;

cin >> poly2;

while (true)

{

system("cls");

cout

switch (selection)

{

case 0:

printMenu();

break;

case 1:

cout

cout

cout

cout

printMenu();

break;

case 2:

polyAdd = poly1 + poly2;

cout

cout

printMenu();

break;

case 3:

polySub = poly1 - poly2;

cout

cout

printMenu();

break;

case 4:

polyMult = poly1 * poly2;

cout

cout

printMenu();

break;

case 5:

polyDiv = poly1 / poly2;

cout

cout

printMenu();

break;

case 6:

polyRemainder = poly1 % poly2;

cout

cout

printMenu();

break;

case 9:

cout

return 0;

default:

cout

printMenu();

}

cin >> selection;

}

}

void printMenu()

{

cout

cout

cout

cout

cout

cout

cout

cout

cout

cout

}

Sample input / output:

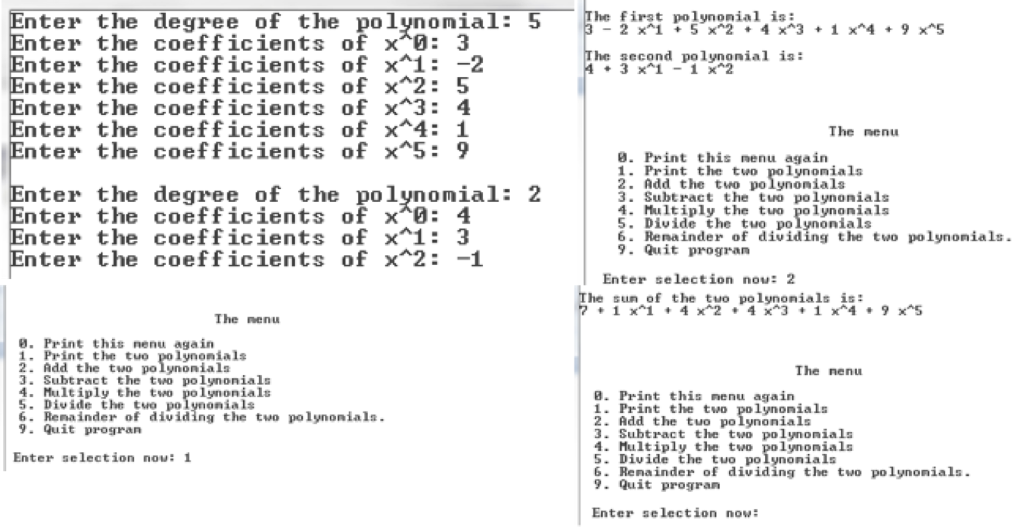
nter the degree of the polynomial: 5 nter the coefficients of x 3 nter the coefficients of x1 -2 nter the coefficients of x 2: 5 nter the coefficients of x 3 4 nter the coefficients of x*4: 1 nter the coefficients of x*5: 9 he first polynonial is he second polynonial is The nenu . Print this nenu again . Print the two polynonials 2. Add the two polynonials 3. Subtract the tuo polynonials 4- Multiply the two polynonials 5. Divide the tuo polynonials 6. Renainder of dividing t he two polynonials. 9. Quit progran nter the degree of the polynonial: 2 Enter the coefficients nter the coefficients of x^1: 3 nter the coefficients of x 2:-1 Enter selection now: 2 The sun of the tuo polynonials is: The nenu . Print this nenu again 1. Print the tuo polynonials 2. Add the tuo polynoniala 3. Subtract the two polynonials 4. Multiply the two polynonials 5. Divide the tuo polynonials 6. Renainder of dividing the two polynonials. 9. Quit progran The nenu 8. Print this nenu again 1. Print the two polynonials 2. Add the tuo polynonials 3. Subtract the two polynonials 4. Hultiply the two polynonials . Divide the tuo polynonials 6. Renainder of dividing the two polynonials. 9. Quit progran Enter selection now: 1 Enter selection now #