Create a new frequency distribution of the Brown bigrams. Plot the cumulative frequency distribution of the top 50 bigrams.

Then do add one smoothing on the bigrams. This will require adding one to all the bigram counts, including those that previously had count 0. You will also need to change the ungram counts appropriately. You will compute all possible bigrams using the known vocabulary, so use the keys of the unigram Brown distribution you created before to compute the set of possible bigrams. The vocabulary size from that exercise should be 49815. Then having added 1 to all the bigram counts, you must compute at least the following Probabilities:

1. P(the | in) before and after smoothing (P_{\text{mle}} and P_{\text{laplace}});

2. P(in the) before and after smoothing;

3. P(said the) before and after smoothing.

4. P(the | said) before and after smoothing.

In some cases you will to use the unigram counts to compute these probabilities. Remember that the unigram counts must change too when smoothing.

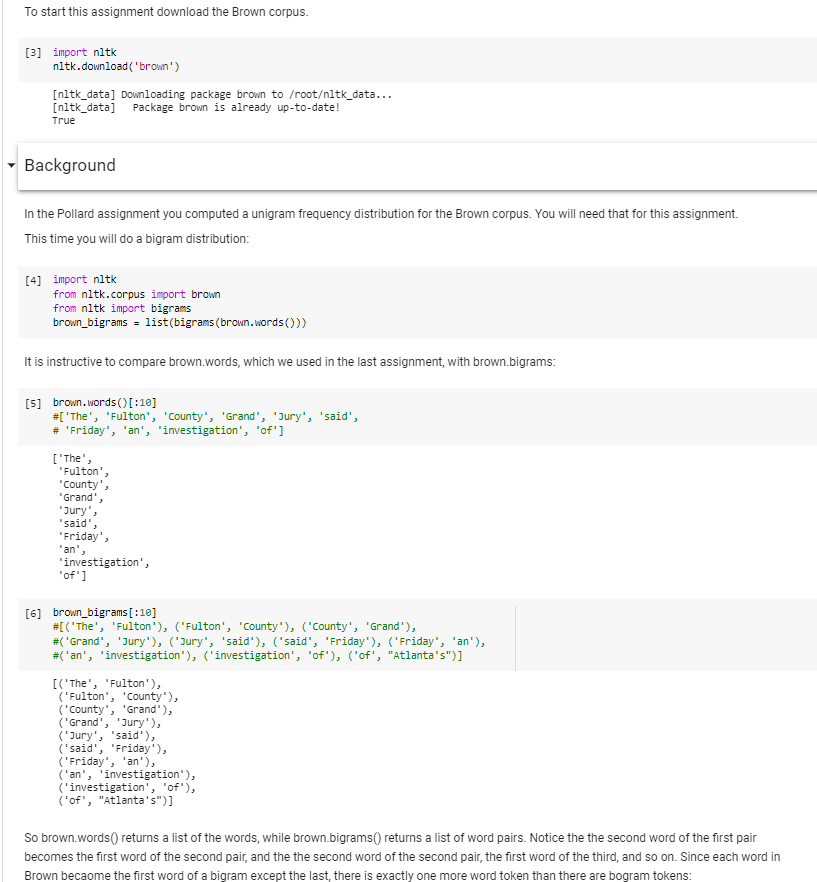
To start this assignment download the Brown corpus. [3] import nitk nitk.download('brown') [nltk_data] Downloading package brown to /rootltk_data... [nltk_data] Package brown is already up-to-date! True Background In the Pollard assignment you computed a unigram frequency distribution for the Brown corpus. You will need that for this assignment. This time you will do a bigram distribution: [4] import nitk from nitk.corpus import brown from nitk import bigrams brown_bigrams = list(bigrams (brown.words()) It is instructive to compare brown.words, which we used in the last assignment, with brown.bigrams: [5] brown.words[:10] #I 'The', 'Fulton', 'County', 'Grand', 'Jury', 'said', # 'Friday', 'an', 'investigation', 'of'] ['The', Fulton', "County's "Grand', Jury', said' 'Friday', 'an', 'investigation', 'of'] [6] brown_bigrams[:10] #[('The', 'Fulton'), ('Fulton', 'County'), ('County', 'Grand'), # "Grand', 'Jury'), ('Jury', 'said'), ('said', 'Friday'), ('Friday', 'an'), #('an', 'investigation'), ('investigation', 'of'), ('of', "Atlanta's")] [('The', 'Fulton'), ('Fulton', 'County'), ('County', 'Grand'), ("Grand', 'Jury'), ('Jury', 'said'), ('said', 'Friday'), ('Friday', 'an'), ('an', 'investigation'), ('investigation', 'of'), ('of", "Atlanta's")] So brown.words() returns a list of the words, while brown.bigrams() returns a list of word pairs. Notice the the second word of the first pair becomes the first word of the second pair, and the the second word of the second pair, the first word of the third, and so on. Since each word in Brown becaome the first word of a bigram except the last, there is exactly one more word token than there are bogram tokens: To start this assignment download the Brown corpus. [3] import nitk nitk.download('brown') [nltk_data] Downloading package brown to /rootltk_data... [nltk_data] Package brown is already up-to-date! True Background In the Pollard assignment you computed a unigram frequency distribution for the Brown corpus. You will need that for this assignment. This time you will do a bigram distribution: [4] import nitk from nitk.corpus import brown from nitk import bigrams brown_bigrams = list(bigrams (brown.words()) It is instructive to compare brown.words, which we used in the last assignment, with brown.bigrams: [5] brown.words[:10] #I 'The', 'Fulton', 'County', 'Grand', 'Jury', 'said', # 'Friday', 'an', 'investigation', 'of'] ['The', Fulton', "County's "Grand', Jury', said' 'Friday', 'an', 'investigation', 'of'] [6] brown_bigrams[:10] #[('The', 'Fulton'), ('Fulton', 'County'), ('County', 'Grand'), # "Grand', 'Jury'), ('Jury', 'said'), ('said', 'Friday'), ('Friday', 'an'), #('an', 'investigation'), ('investigation', 'of'), ('of', "Atlanta's")] [('The', 'Fulton'), ('Fulton', 'County'), ('County', 'Grand'), ("Grand', 'Jury'), ('Jury', 'said'), ('said', 'Friday'), ('Friday', 'an'), ('an', 'investigation'), ('investigation', 'of'), ('of", "Atlanta's")] So brown.words() returns a list of the words, while brown.bigrams() returns a list of word pairs. Notice the the second word of the first pair becomes the first word of the second pair, and the the second word of the second pair, the first word of the third, and so on. Since each word in Brown becaome the first word of a bigram except the last, there is exactly one more word token than there are bogram tokens