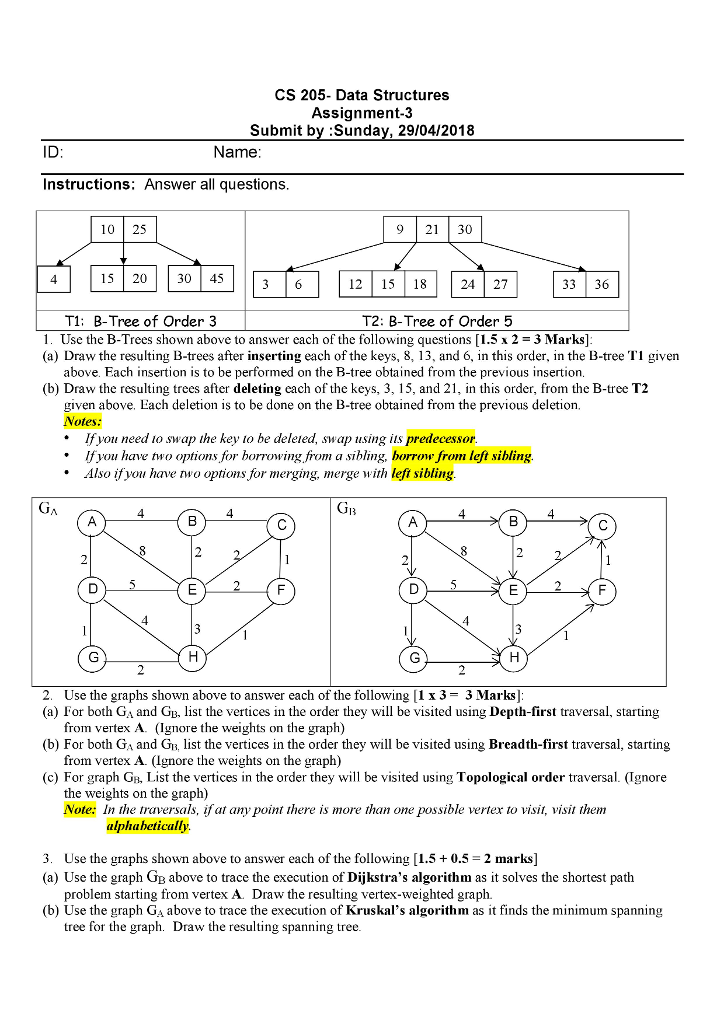
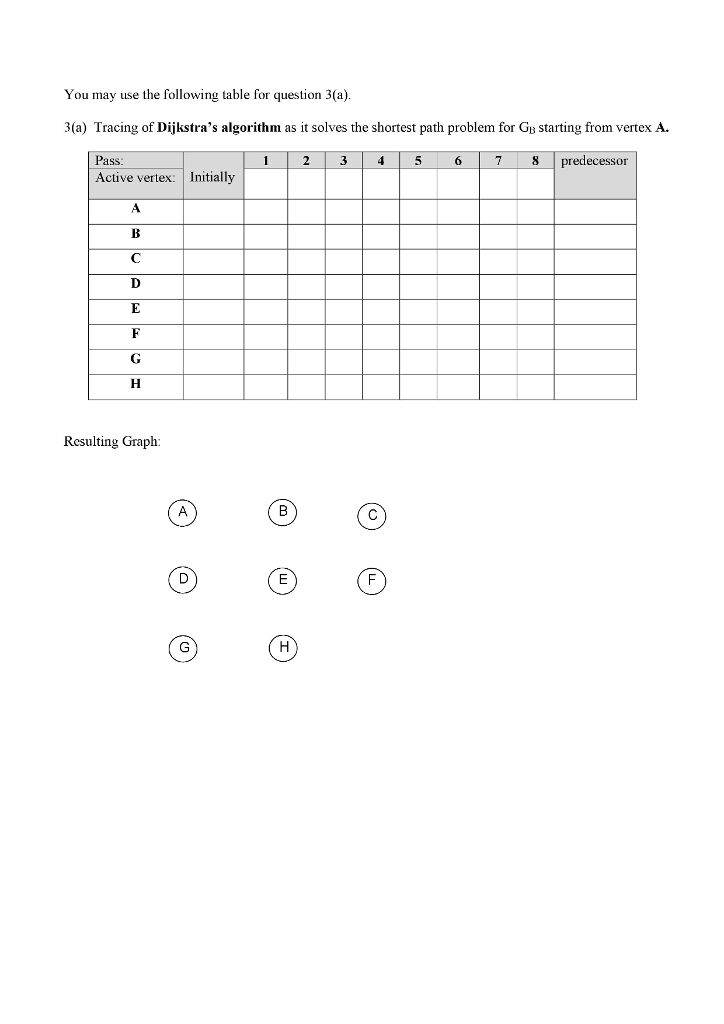
CS 205- Data Structures Assignment-3 Submit by Sunday, 29/04/2018 ID Name Instructions: Answer all questions 10 25 9 2130 15 20 3045 12 1518 24 27 33 36 T1: B-Tree of Order 3 12: B-T ree of Order 5 1 . Use the B-Trees shown above to answer each of the following questions [ 1.5 x 2 = 3 Marks] (a) Draw the resulting B-trees after inserting each of the keys, 8, 13, and 6, in this order, in the B-tree T1 given above. Each insertion is to be performed on the B-tree obtained from the previous insertion (b) Draw the resulting trees after deleting each of the keys, 3, 15, and 21, in this order, from the B-tree T2 given above. Each deletion is to be done on the B-tree obtained from the previous deletion. If you need io swap the key to be deleied, swap using its predecessor If you have two options for borrowing from a sibling, borrow from left sibling *Also ifyou have rwo options for merging, merge with left sibling 2. (a) For both GA and GB, list the vertices in the order they will be visited using Depth-first traversal, starting (b) For both Ga and GB, list the vertices in the order they will be visited using Breadth-first traversal, starting (c) For graph GB, List the vertices in the order they will be visited using Topological order traversal. (Ignore Use the graphs shown above to answer each of the following [1 x 3-3 Marks] from vertex A. (Ignore the weights on the graph) from vertex A. (lgnore the weights on the graph) the weights on the graph) Note: In the traversals, if at any point there is more than one possible verter to visit, visit them alphahetically 3. Use the graphs shown above to answer each of the following [1.5 0.5 2 marks] (a) Use the graph GB above to trace the execution of Dijkstra's algorithm as it solves the shortest path problem starting from vertex A Draw the resulting vertex-weighted graph. (b) Use the graph GA above to trace the execution of Kruskal's algorithm as it finds the minimum spanning tree for the graph. Draw the resulting spanning tree