d $=$ DisjointForests$(10)$

for i in range$(10)$:

d$.$make$\_$set$($i$)$

for i in range$(10)$:

assert d$.$find$($i$)==$ i$,$ f'Failed: Find on $\{$i$\}$ must return $\{$i$\}$ back'

d$.$union$(0,1)$

d$.$union$(2,3)$

assert$($d$.$find$(0)==$ d$.$find$(1)),\text{'}0$ and $1$ have been union$-$ed together'

assert$($d$.$find$(2)==$ d$.$find$(3)),\text{'}2$ and $3$ have been union$-$ed together'

assert$($d$.$find$(0)!=$ d$.$find$(3)),\text{'}0$ and $3$ should be in different trees'

assert$(($d$.$get$\_$rank$(0)==2$ and d$.$get$\_$rank$(1)==1)$ or

$($d$.$get$\_$rank$(1)==2$ and d$.$get$\_$rank$(0)==1)),$ 'one of the nodes $0$ or $1$ must have rank $2\text{'}$

assert$(($d$.$get$\_$rank$(2)==2$ and d$.$get$\_$rank$(3)==1)$ or

$($d$.$get$\_$rank$(3)==2$ and d$.$get$\_$rank$(2)==1)),$ 'one of the nodes $2$ or $3$ must have rank $2\text{'}$

d$.$union$(3,4)$

assert$($d$.$find$(2)==$ d$.$find$(4)),\text{'}2$ and $4$ must be in the same set in the family.$\text{'}$

d$.$union$(5,7)$

d$.$union$(6,8)$

d$.$union$(3,7)$

d$.$union$(0,6)$

assert$($d$.$find$(6)==$ d$.$find$(1)),\text{'}1$ and $6$ must be in the same set in the family'

assert$($d$.$find$(7)==$ d$.$find$(4)),\text{'}7$ and $4$ must be in the same set in the family'

print$(\text{'}$All tests passed: $10$ points.$\text{'})$

AssertionError Traceback $($most recent call last$)$

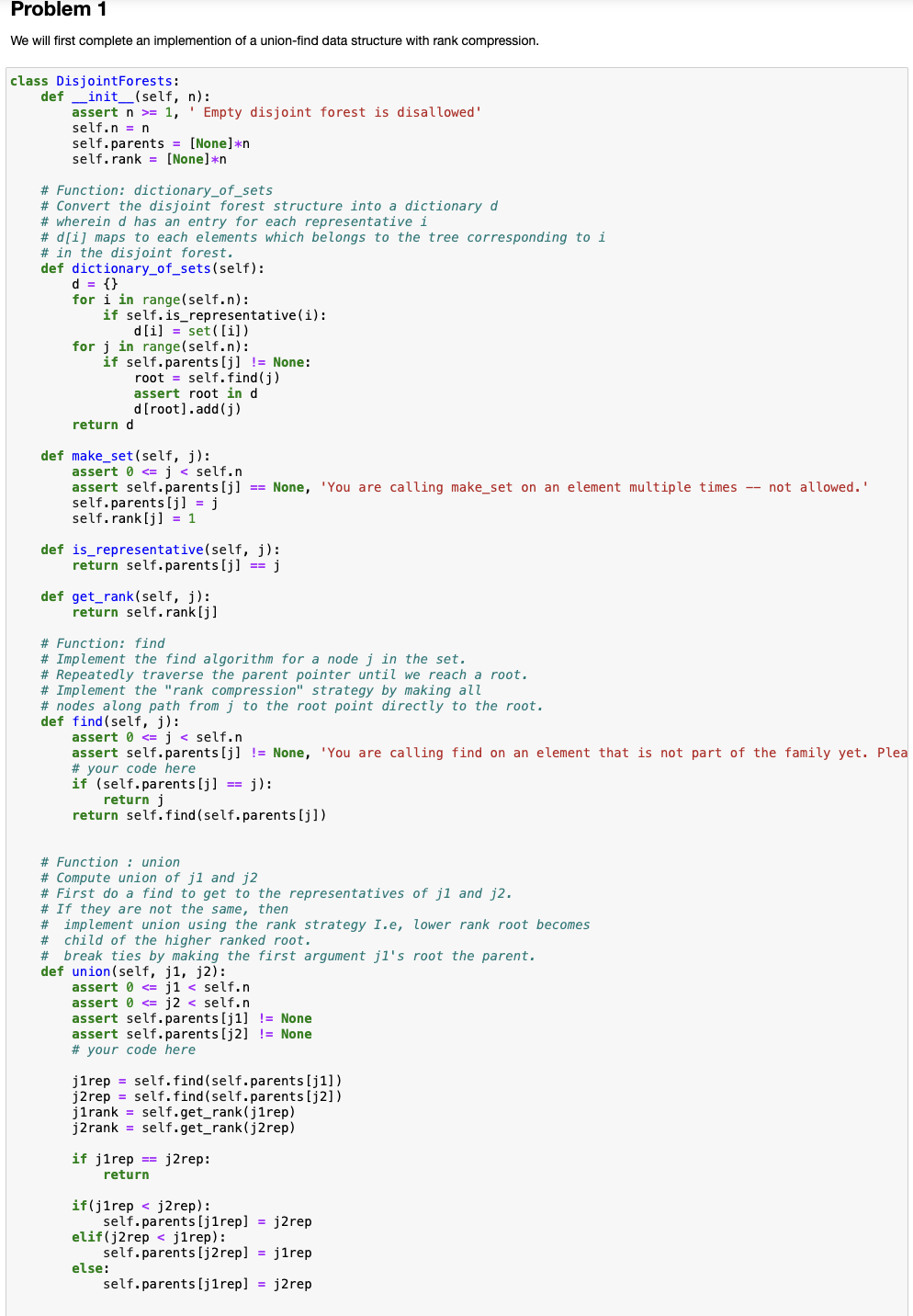
We will first complete an implemention of a union$-$find data structure with rank compression.

class DisjointForests:

def $($self$,$ n$)$:

assert n $>=1,\text{'}$ Empty disjoint forest is disallowed'

self.n $=$ n

self.parents $=[$None$]*$n

self.rank $=[$None$]*$nConvert the disjoint forest structure into a dictionary dd$[$i$]$ maps to each elements which belongs to the tree corresponding to idef dictionary$\_$of$\_$sets$($self$)$:

d $=\{\}$

for i in range$($self$.$n$)$:

if self.is$\_$representative$($i$)$:

d$[$i$]=$ set$([$i$])$

for j in range$($self$.$n$)$:

if self.parents$[$j$]!=$ None:

root $=$ self.find$($j$)$

assert root in d

d$[$root$].$add$($j$)$

return d

def make$\_$set$($self$,$ j$)$:

assert j $$ self.n

assert self.parents$[$j$]==$ None, 'You are calling make$\_$set on an element multiple times $--$ not allowed.$\text{'}$

self.parents$[$j$]=$ j

self.rank$[$j$]=1$

def is$\_$representative$($self$,$ j$)$:

return self.parents$[$j$]==$ j

def get$\_$rank$($self$,$ j$)$:

return self.rank$[$j$]$Implement the find algorithm for a node j in the set.Implement the "rank compression" strategy by making alldef find$($self$,$ j$)$:

assert j $$ self.n

assert self.parents$[$j$]!=$ None, 'You are calling find on an element that is not part of the family yet. Pleaif $($self$.$parents$[$j$]==$ j$)$:

return j

return self.find$($self$.$parents$[$j$])$Compute union of j$1$ and j$2$If they are not the same, thenchild of the higher ranked root.def union$($self$,$ j$1,$ j$2)$:

assert j$1$ self.n

assert j$2$ self.n

assert self.parents$[$j$1]!=$ None

assert self.parents$[$j$2]!=$ Nonej$1$rep $=$ self.find$($self$.$parents$[$j$1])$

j$2$rep $=$ self.find$($self$.$parents$[$j$2])$

j$1$rank $=$ self.get$\_$rank$($j$1$rep$)$

j$2$rank $=$ self.get$\_$rank$($j$2$rep$)$

if j$1$rep $==$ j$2$rep:

return

if$($j$1$rep $$ j$2$rep$)$:

self.parents$[$j$1$rep$]=$ j$2$rep

elif$($j$2$rep $$ j$1$rep$)$:

self.parents$[$j$2$rep$]=$ j$1$rep

else:

self.parents$[$j$1$rep$]=$ j$2$rep